Calendar for 2022 - 2023 Fall Semester MATH 2301 Calculus I
Lecture Sections 172 and Recitation Sections 173, 174, 175, 176
(taught by Mark Barsamian)
Week 1 (Mon Aug 22 through Fri Aug 26)
Book Sections and (Homework Exercises)
- Section 1.1 An Introduction to Limits (#2, 3, 4, 7-15odd, 21, 23, 27)
- Section 1.3 Finding Limits Analytically (#1, 2, 4, 5, 7-18, 19-33odd, 35-38, 39, 43)
Mon Aug 22 Meeting Topics
Discussion of Functions and Function Notation (Chapter 1)
- Piecewise-Defined Functions
Consider this symbol:
$$ f(x) = \left\{ \begin{array}{ll} -2x+10, & \quad x\leq 3 \\ x^2, & \quad x>3 \end{array} \right. $$- What does this symbol mean? How is it spoken?
- What is \( f(2) \)? Why?
- What is \( f(3) \)? Why?
- What is \( f(4) \)? Why?
- What does the graph of \( f(x) \) look like? How can we figure it out?
- The Absolute Value Function
You're all familiar with the behavior of the absolute value when the thing inside is a number.
- What is \( |5| \)?
- What is \( |-7| \)?
- What is \( |0| \)?
Based on that familiarity, you might feel like you understand the absolute value. But do you understand the absolute value function?
- What does the graph of \( |x| \) look like? How can we figure it out?
- Can you express \( |x| \) as a piecewise-defined function?
- What does the graph of $$ \frac{|x|}{x} $$ look like? How can we figure it out?
- Can you express $$ \frac{|x|}{x} $$ as a piecewise-defined function?
- The Important and Subtle Issue of Cancelling Terms in Expressions
Consider the following two functions:
$$ f(x) = \frac{x^2-2x-3}{x-3} = \frac{(x-3)(x+1)}{(x-3)} $$ $$ g(x) = x+1 $$- What does the graph of \( g(x) \) look like?
- What does the graph of \( f(x) \) look like?
Are those really two different functions, or are they actually the same function? That is, can we always cancel terms such as \( \frac{(x-3)}{(x-3)}\) in expressions? What do the students have to say about this? If a student has an opinion, can they explain a bit about why they have that opinion?
Conclusions about the functions \(f(x)\) and \(g(x)\)
Functions \(f(x)\) and \(g(x)\) are not the same function, because they do not have the same domain. Observe that $$g(3)=4$$ $$f(3)= \ does \ not \ exist$$ The reason that \(f(3)\) does not exist is that $$ f(3) = \frac{((3)-3)((3)+1)}{((3)-3)} = \frac{(0)(4)}{(0)} = \frac{0}{0} \ (undefined)$$ and division by \(0\) is not defined. Put another way, one cannot cancel \(\frac {0}{0}\).
So in general, one cannot replace the expression $$ \frac{x^2-2x-3}{x-3} = \frac{(x-3)(x+1)}{(x-3)} $$ with the simplified expression $$ x+1 $$ This may be contrary to what you have been told in previous courses, and even what you may be asked to do in MyLab. That is, you may be told to simplify the expression $$ \frac{x^2-2x-3}{x-3} = \frac{(x-3)(x+1)}{(x-3)} $$ with the expectation that the simplified version is $$ x+1 $$ But this is incorrect. That is, without any information about the value of \(x\), one is not allowed to do that simplification!!
However, if you somehow know (or are told) that \(x\neq 3\), then you can replace the expression $$ \frac{x^2-2x-3}{x-3} = \frac{(x-3)(x+1)}{(x-3)} $$ with the simplified expression $$ x+1 $$ That is because when \(x\neq 3\), the value of \( f(x)\) will always be the same as the value of \(g(x)\). But if you do know that \(x\neq 3\), and you use that information to replace the expression $$ \frac{x^2-2x-3}{x-3} = \frac{(x-3)(x+1)}{(x-3)} $$ with the simplified expression $$ x+1 $$ then you should explain clearly that you are allowed to do the cancellation because you know that \(x\neq 3\), which tells you that \(x - 3 \neq 0\), which means that you can cancel \(\frac {(x-3)}{(x-3)}\).
Fussing over whether one can or cannot cancel terms in an expression, and explaining why, may seem to be over-thinking what ought to just be simple math. But Calculus is not simple math, and the issue of whether or not one can cancel terms is one of the most important concepts of the first month of the course!!.
Tue Aug 23 Meeting Topics
Introduction to Limits (Book Section 1.1)
A printed Definition of Limit was distributed.
Students worked on Group Work GW01 (Limits for a Function Given by a Graph).
Students worked on Group Work GW02 (Guessing Limits for a Function Given by a Formula by Plugging in Numbers).
Wed Aug 24 Meeting Topics
Introduction to Limits (Book Section 1.1)
Fri Aug 26 Meeting Topics
Finding Limits Analytically (Book Section 1.3)
A printed Class ActivityClass Activity
We discussed a Student's Solution to Homework Exercise 1.1#11 that they sent to Mark B when asking for help. (Mark B. would like to profoundly thank the student for letting us discuss their solution during class. Their solution provided the inspiration for the entire meeting outline.)
Week 2 (Mon Aug 29 through Fri Sep 2)
Book Sections and (Homework Exercises)
- Section 1.3 Finding Limits Analytically (#1, 2, 4, 5, 7-18, 19-33odd, 35-38, 39, 43)
- Section 1.4 One Sided Limits (#1-12, 13-21odd)
Mon Aug 29 Meeting Topics
Continuing Discussion of Finding Limits Analytically (Book Section 1.3)
We discussed a Student's Solution to Homework Exercises from Section 1.1 that they sent to Mark B when asking for help. (Mark B. would like to thank the student for letting us discuss their solution during class..)
A printed Worksheet about the Squeeze Theorem was distributed.
Quiz Q01 on Tue Aug 30 Covering Section 1.1
- 20 Minutes at the end of class
- No Calculators
- Similar to GW01 and Suggested Exercises 1.1#7-13 about computing \(y\) values and estimating limits for function given by a formula.
Tue Aug 30 Meeting Topics
Finding Limits Analytically (Book Sections 1.3)
Students worked Group Work GW04 (Finding Limits).
Quiz Q01 During Tue Aug 30 Meeting Covering Section 1.1
- 20 Minutes at the end of class
- No Calculators
- Similar to GW01 and Suggested Exercises 1.1#7-13 about computing \(y\) values and estimating limits for function given by a formula.
Wed Aug 31 Meeting Topics
One Sided Limits (Book Section 1.3)
Fri Sep 2 Meeting Topics
Class Presentations for Fri Sep 2
Nana Asare CP1: Present a solution to book exercise 1.3#30. $$\lim_{x \rightarrow 0} \frac {x^2-7x}{x^2+2x}$$ Note that this is an exercise from Section 1.3, so you should be finding the limit by using the Theorems about Limit Properties that are presented in the book in Section 1.3.
- To prepare for the presentation, study Example 1.3.16 in Book Section 1.3 and also study your Class Notes and Recitation Notes.
- Prepare your presentation according to the Presentation Guidelines.
Tyler Boldon CP1: Present a solution to book exercise 1.3#32 $$\lim_{x \rightarrow -8} \frac {x^2+3x-40}{x^2+13x+40}$$ Note that this is an exercise from Section 1.3, so you should be finding the limit by using the Theorems about Limit Properties that are presented in the book in Section 1.3.
- To prepare for the presentation, study Example 1.3.16 in Book Section 1.3 and also study your Class Notes and Recitation Notes.
- Prepare your presentation according to the Presentation Guidelines.
Ellie BowerCP1: Find the limit using Section 1.3 techniques. That is, find the limit by using the Theorems about Limit Properties that are presented in the book in Section 1.3. $$\lim_{x \rightarrow 36} \frac {x-36}{\sqrt{x}-6}$$
- To prepare for the presentation, study Example 1.3.17 in Book Section 1.3 and also study your Class Notes and Recitation Notes.
- Prepare your presentation according to the Presentation Guidelines.
Andrew Champagne CP1: Find the limit using Section 1.3 techniques. That is, find the limit by using the Theorems about Limit Properties that are presented in the book in Section 1.3. $$\text{For } f(x)=-x^2+10x \\ \text{find } \lim_{h \rightarrow 0} \frac {f(4+h)-f(4)}{h}$$
- To prepare for the presentation, study Example 1.3.18 in Book Section 1.3 and also study your Class Notes and Recitation Notes.
- Prepare your presentation according to the Presentation Guidelines.
Drew Conway CP1: Present a solution to book exercise 1.4#16 $$f(x)=\begin{cases}\cos (x) & \text{if }x \lt \pi \\ \sin (x) & \text{if }x\geq \pi \end{cases} $$
- Find \(lim_{x \rightarrow \pi^-} f(x) \)
- Find \(lim_{x \rightarrow \pi^+} f(x) \)
- Find \(lim_{x \rightarrow \pi} f(x) \)
- Find \(f(\pi) \)
- Illustrate with a graph of \(f(x)\)
- To prepare for the presentation, study the examples in Book Section 1.4 and also study your Class Notes.
- Prepare your presentation according to the Presentation Guidelines.
Mark will briefly discuss Continuity (Book Section 1.4)
Handed out Reference R03 The Intermediate Value Theorem
Week 3 (Mon Sep 5 through Fri Sep 9)
Book Sections and (Homework Exercises)
- Section 1.5 Continuity (#1-22, 23-38odd)
- Section 1.6 Limits Involving Infinity (#1-14, 19-28)
Mon Sep 5 is Labor Day: No Class
Tue Sep 6 Meeting Topics
Continuity (Book Section 1.5)
Class Presentations Involving Continuity for Tue Sep 6
Student #6 CP1: Present a solution to book exercise 1.5#20 $$f(x)=\begin{cases}x^2 - x^2 & \text{if }x \lt 1 \\ x-2 & \text{if }x\geq 1 \end{cases} $$ Without making a graph of \(f(x)\), answer the following two questions:
- Is \(f\) continuous at \(0\)? Explain.
- Is \(f\) continuous at \(1\)? Explain.
- To prepare for the presentation, study The beginning of Book Section 1.5. The problem that you have to solve has no similar examples in the book. But to solve your problem, you only need to study the Definition 1.5.1 of Continuous Functions and to note that immediately following that definition, there is a procedure that you can follow to establish whether or not a function \(f\) is continuous at \(x=c\).
- Prepare your presentation according to the Presentation Guidelines.
Student #7 CP1: Present a solution to book exercise 1.5#24. For the function $$f(x)=\sqrt{x^2-25}$$ give the intervals on which \(f\) is continuous.
- To prepare for the presentation, study Book Section 1.5 through Example 1.5.10. Your problem is similar to Examples 1.5.7 and 1.5.10.
- Prepare your presentation according to the Presentation Guidelines.
Student #8 CP1: Present a solution to book exercise 1.5#28. For the function $$g(t)=\frac{1}{\sqrt{9-t^2}}$$ give the intervals on which \(g\) is continuous.
- To prepare for the presentation, study Book Section 1.5 through Example 1.5.10. Your problem is similar to Examples 1.5.7 and 1.5.10.
- Prepare your presentation according to the Presentation Guidelines.
Student Number assignments:
- In Section 173 (Tue 9:30)
- Amy Evers is Student #6
- Dalana Goddard is Student #7
- Lauren Hartel is Student #8
- In Section 174 (Tue 11:00)
- Carly Doros is Student #6
- Nicole Grant is Student #7
- Tim Jaskiewicz is Student #8
- In Section 175 (Tue 2:00)
- Evan Green is Student #6
- Kierston Harper is Student #7
- Olivia Keener is Student #8
- In Section 176 (Tue 3:30)
- Carlotta Dattilo is Student #6
- Paul Gbadebo is Student #7
- Alan Romero Herrera is Student #8
Limits Involving Infinity (Book Section 1.6)
Discussed Reference R04 (Limits Involving Infinity).
Students worked Group Work GW05 (Limits Involving Infinity for a function given by a graph).
Quiz Q02 on Wed Sep 7 Covering Sections 1.3, 1.4
Wed Sep 7 Meeting Topics
Limits Involving Infinity (Book Section 1.6)
Quiz Q02 on Wed Sep 7 Covering Sections 1.3, 1.4
Fri Sep 9 Meeting Topics
Limits Involving Infinity (Book Section 1.6)
Introduction
Today, we're discussing infinite limits. That, is, limits such as
$$\lim_{x\rightarrow c^-} f(x) = \infty \\ \lim_{x\rightarrow c} f(x) = -\infty$$The book gives only a precise definition of infinite limits, a definition involving N and delta. This is the same style of definition as the book's initial definition of regular limits in Section 1.2, a definition involving epsilon and delta. There is nothing wrong with the book's precise definitions, but what is lacking in the book's presentation of limits is an inf ormal definition of limits, both regular limits and infinite limits.
For our course, there are two Reference Pages about limits, posted on the Course Web Page, that show the book's precise definitions of regular limits and of infinite limits, along with informal definitions of those limits. Here are links to those two Reference Pages.
- R01: Definition of Limit was distributed on Tue Aug 23.
- R04: Limits Involving Infinity was discussed Fri Sep 9.
The precise definitions of limits are above the level of MATH 2301, but the informal definition of limits (both kinds) are appropriate for a class at the level of MATH 2301. Furthermore, he gave an example of computing limits, both regular limits and infinite limits, using what could be called an informal method.
The informal method of computing the limit of an expression involves examining the trends in the various terms in the expression, and making a conclusion about the trend in the value of the expression.
[Example 1] we will revisit the following function, which was studied in Group Work GW02: Guessing Limits for a Function Given by a Formula by Plugging in Numbers on Tue Aug 23.
$$f(x)=\frac{x^2-3x}{x^2-5x+6}=\frac{x(x-3)}{(x-2)(x-3)}$$(a) find \(lim_{x \rightarrow 3^-}f(x)\) by using the informal method of computing the limit. That is, by considering the trends in the size of the factors. Use the Expanded Definition of Limit, Involving Infinity, if appropriate.
First we note that because \(x \rightarrow 3^-\), we know that \(x \neq 3\), so \(x-3 \neq 0\). Therefore, we can cancel the \(\frac{(x-3)}{(x-3)}\) terms.
$$lim_{x \rightarrow 3^-}f(x)=lim_{x \rightarrow 3^-}\frac{x(x-3)}{(x-2)(x-3)}=lim_{x \rightarrow 3^-}\frac{x}{(x-2)}$$Now, because \(x \rightarrow 3^-\), we know that
- The numerator, \(x\), is getting closer and closer to \(3\).
- The denominator, \(x-2\), is getting closer and closer to \(1\).
- Therefore, the ratio is getting closer and closer to \(3\).
That is, when the trend in the \(x\) values is that \(x\) is getting closer and closer to \(3\) but less than \(3\), the trend in the values of \(f(x)\) will be that \(f(x)\) is getting closer and closer to \(3\). In limit notation, these trends are denoted as follows.
$$lim_{x \rightarrow 3^-}f(x)=lim_{x \rightarrow 3^-}\frac{x(x-3)}{(x-2)(x-3)}=lim_{x \rightarrow 3^-}\frac{x}{(x-2)}=3$$(b) find \(lim_{x \rightarrow 2^-}f(x)\) by using the informal method of computing the limit. That is, by considering the trends in the size of the factors. Use the Expanded Definition of Limit, Involving Infinity, if appropriate.
We note that because \(x \rightarrow 2^-\), we know that \(x \neq 3\), so \(x-3 \neq 0\). Therefore, we can cancel the \(\frac{(x-3)}{(x-3)}\) terms.
$$lim_{x \rightarrow 2^-}f(x)=lim_{x \rightarrow 2^-}\frac{x(x-3)}{(x-2)(x-3)}=lim_{x \rightarrow 2^-}\frac{x}{(x-2)}$$Now, because \(x \rightarrow 2^-\), we know that
- The numerator, \(x\), is getting closer and closer to \(2\).
- The denominator, \(x-2\), is getting closer and closer to \(0\) but is negative.
- Therefore, the ratio will be a huge negative number.
- The closer that \(x\) gets to \(2\), while remaining less than \(2\), the more huge and negative will be the value of the ratio.
That is, when the trend in the \(x\) values is that \(x\) is getting closer and closer to \(2\) but less than \(2\), the trend in the values of \(f(x)\) will be that \(f(x)\) is getting huge and negative, without bound. In limit notation, these trends are denoted as follows.
$$lim_{x \rightarrow 2^-}f(x)=lim_{x \rightarrow 2^-}\frac{x(x-3)}{(x-2)(x-3)}=lim_{x \rightarrow 2^-}\frac{x}{(x-2)}=-\infty$$Notice that if we were using the Original Definition of Limit, we would said instead that the limit does not exist.
End of [Example 1]
[Example 2] we will revisit the following function, which was studied in Group Work GW03: Function Values and Limits for a Rational Function on Fri, Aug 26.
$$f(x)=\frac{x^2+10x+21}{x^2+5x+6}=\frac{(x+7)(x+3)}{(x+2)(x+3)}$$(a) find \(lim_{x \rightarrow -3^+}f(x)\) by using the informal method of computing the limit. That is, by considering the trends in the size of the factors. Use the Expanded Definition of Limit, Involving Infinity, if appropriate.
First we note that because \(x \rightarrow -3^+\), we know that \(x \neq 3\), so \(x+3 \neq 0\). Therefore, we can cancel the \(\frac{(x+3)}{(x+3)}\) terms.
$$lim_{x \rightarrow -3^+}f(x)=lim_{x \rightarrow -3^+}\frac{(x+7)(x+3)}{(x+2)(x+3)}=lim_{x \rightarrow -3^+}\frac{(x+7)}{(x+2)}$$Now, because \(x \rightarrow -3^+\), we know that
- The numerator, \(x+7\), is getting closer and closer to \(4\).
- The denominator, \(x+2\), is getting closer and closer to \(-1\).
- Therefore, the ratio is getting closer and closer to \(-4\).
That is, when the trend in the \(x\) values is that \(x\) is getting closer and closer to \(-3\) but greater than \(-3\), the trend in the values of \(f(x)\) will be that \(f(x)\) is getting closer and closer to \(-4\). In limit notation, these trends are denoted as follows.
$$lim_{x \rightarrow -3^+}f(x)=lim_{x \rightarrow -3^+}\frac{(x+7)(x+3)}{(x+2)(x+3)}=lim_{x \rightarrow -3^+}\frac{(x+7)}{(x+2)}=-4$$(b) find \(lim_{x \rightarrow -2^+}f(x)\) by using the informal method of computing the limit. That is, by considering the trends in the size of the factors. Use the Expanded Definition of Limit, Involving Infinity, if appropriate.
We note that because \(x \rightarrow -2^+\), we know that \(x \neq -3\), so \(x+3 \neq 0\). Therefore, we can cancel the \(\frac{(x+3)}{(x+3)}\) terms.
$$lim_{x \rightarrow -3^+}f(x)=lim_{x \rightarrow -3^+}\frac{(x+7)(x+3)}{(x+2)(x+3)}=lim_{x \rightarrow -3^+}\frac{(x+7)}{(x+2)}$$Now, because \(x \rightarrow -2^+\), we know that
- The numerator, \(x+7\), is getting closer and closer to \(5\).
- The denominator, \(x+2\), is getting closer and closer to \(0\) but is positive.
- Therefore, the ratio will be a huge positive number.
- The closer that \(x\) gets to \(-2\), while remaining greater than \(-2\), the more huge and positive will be the value of the ratio.
That is, when the trend in the \(x\) values is that \(x\) is getting closer and closer to \(-2\) but greater than \(2\), the trend in the values of \(f(x)\) will be that \(f(x)\) is getting huge and positive, without bound. In limit notation, these trends are denoted as follows.
$$lim_{x \rightarrow -2^+}f(x)=lim_{x \rightarrow -2^+}\frac{(x+7)(x+3)}{(x+2)(x+3)}=lim_{x \rightarrow -2^+}\frac{(x+7)}{(x+2)}=\infty $$Notice that if we were using the Original Definition of Limit, we would said instead that the limit does not exist.
End of [Example 2]
Week 4 (Mon Sep 12 through Fri Sep 16)
Book Sections and (Homework Exercises)
- Section 2.1 Instantaneous Rates of Change: The Derivative (1-22, 27-36)
Mon Sep 12 Meeting Topics
Limits Involving Infinity (Book Section 1.6)
On Fri Sep 9, Mark discussed infinite limits. He presented two Reference Pages about limits, posted on the Course Web Page. These Reference Pages show the book's precise definitions of regular limits and of infinite limits, along with informal definitions of those limits. Here are links to those two Reference Pages.
- R01: Definition of Limit was distributed on Tue Aug 23.
- R04: Limits Involving Infinity was discussed Fri Sep 9.
Mark also discussed an informal method of computing the limit of an expression. This method involves examining the trends in the various terms in the expression, and making a conclusion about the trend in the value of the expression. The method works equally well for limits that turn out to be numbers and limits that turn out to be infinite.
See the Calendar entry for Fri Sep 9 to see the discussion of the informal method of computing the limit and to see some examples of its use.
We'll start today with three presentations involving using that method to find limits of very similar-looking rational functions.
Class Presentations Involving the Informal Method for Computing Limits for Mon Sep 12
Ben Oldiges CP1 Let \(f(x)\) be the following function.
$$f(x)=\frac{7x^2-49x+70}{3x^2-27x+60}=\frac{7(x-2)(x-5)}{3(x-1)(x-5)}$$(Find \(lim_{x \rightarrow 5^+}f(x)\) by using the informal method of computing the limit. That is, by considering the trends in the size of the factors. Use the Expanded Definition of Limit, Involving Infinity, if appropriate.
Austin Kiggins CP1 Let \(g(x)\) be the following function.
$$g(x)=\frac{7x^3-84x^2+315x-350}{3x^2-27x+60}=\frac{7(x-2)(x-5)^2}{3(x-1)(x-5)}$$Find \(lim_{x \rightarrow 5^+}g(x)\) by using the informal method of computing the limit. That is, by considering the trends in the size of the factors. Use the Expanded Definition of Limit, Involving Infinity, if appropriate.
Kelly Koenig CP1 Let \(h(x)\) be the following function.
$$f(x)=\frac{7x^2-49x+70}{3x^3-42x^2+195x-300}=\frac{7(x-2)(x-5)}{3(x-1)(x-5)^2}$$Find \(lim_{x \rightarrow 5^+}h(x)\) by using the informal method of computing the limit. That is, by considering the trends in the size of the factors. Use the Expanded Definition of Limit, Involving Infinity, if appropriate.
Observe that all three of the limits in the presentations were of \(\frac{0}{0}\) indeterminate form. We see that their limits turned out very differently!
Mark will Present Conclusions about General Trends in limits of the form \( \lim_{x\rightarrow c}f(x)\), where \(c\) is a real number and \(f(x)\) is a rational function.
Mark will Discuss limits of the form \( \lim_{x\rightarrow \infty}f(x)\), where \(f(x)\) is a rational function.
Tue Sep 13 Meeting Topics
Topic: Limits Involving Infinity for a Rational Function (Book Section 1.6)
Group Work: Students worked onGroup Work GW06 (Limits Involving Infinity for a Rational Function). (GW06 Solutions)
Exam X1 Covering Chapter 1 on Wed Sep 14
Information for MATH 2301 (Barsamian) Exam X1 Covering Chapter 1
- Exam is on Wed Sep 13, 2022, for the full duration of the class period, 12:55pm - 1:50pm, in Porter 100
- No Calculators, no Cell Phones, No Books, No Notes
- The Exam is 9 problems, 20 points each.
- Compute limits and function values for a function given by graph. (concepts from Sections 1.1 and 1.6)
- Compute the limit of a function involving trigonometric or logarithmic functions. (concepts from Section 1.3)
- Compute a limit requiring use of the Squeeze Theorem. (concepts from Section 1.3)
- Compute a limit involving factoring or multiplying by the conjugate. (concepts from Section 1.3)
- Compute the limit of a difference quotient. (concepts from Section 1.3)
- Compute the limit of a piecewise-defined function. (concepts from Section 1.4)
- Find the intervals where a function is continuous. (concepts from Section 1.5)
- Compute limits that may or may not be infinite, and find vertical asymptotes for a rational function. (concepts from Section 1.6)
- Compute limits at infinity and find horizontal asymptotes for a rational function. (concepts from Section 1.6)
Fri Sep 16 Meeting Topics
Instantaneous Rates of Change: The Derivative (Book Section 2.1)
New Concepts for Today
Definition of the Derivative
- Words: the derivative of \(f(x)\)
- Symbol: \(f'(x)\)
- Meaning: \(f'(x) = \lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}\)
Definition of the Tangent Line
- Words: the line tangent to the graph of \(f(x)\) at \(x=a\)
- Meaning: the line that has these two properties:
- The line contains the point \((a,f(a))\).
- The line has slope \(m=f'(a)\).
The Point Slope Form of the Equation of a Line
If a line that has these two properties:
- The line contains the point \((a,b)\).
- the line has slope \((m\).
The Point Slope Form of the Equation of the Tangent Line
Since the tangent line that has these two properties:
- The line contains the point \((a,f(a))\).
- the line has slope \(m=f'(a)\).
Class Presentations Involving Computing Derivatives for Fri Sep 16
Jonah Lewis CP1 Let \(f(x)\) be the following function.
$$f(x)=5x-11$$The goal is to find the Derivative, \(f'(x)\), using the Definition of the Derivative. That is, the goal is to find this limit:
$$f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$$- Find \(f(x+h)\).
- Find \(f(x+h)\)-\(f(x)\) and simplify your answer.
- Find \(\frac{f(x+h)-f(x)}{h}\) and simplify your answer, assuming that \(h\neq 0\).
- Finally, find \(f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}\).
Dylan Pohovey CP1 Let \(f(x)\) be the following function.
$$f(x)=5x^2-11x+13$$The goal is to find the Derivative, \(f'(x)\), using the Definition of the Derivative. That is, the goal is to find this limit:
$$f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$$Use as your model Example 2.1.17 in the book. Show all details and explain key steps.
Reggie Shaffer CP1 Let \(f(x)\) be the following function.
$$f(x)=\frac{1}{x+7}$$The goal is to find the Derivative, \(f'(x)\), using the Definition of the Derivative. That is, the goal is to find this limit:
$$f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$$Use as your model Example 2.1.18 in the book. Show all details and explain key steps.
Week 5 (Mon Sep 19 through Fri Sep 23)
Book Sections and (Homework Exercises)
- Section 2.1 Instantaneous Rates of Change: The Derivative (#1-22, 27-36)
- Section 2.2 Interpretations of the Derivative (#1-18)
- Section 2.3 Basic Differentiation Rules (#1-38)
Mon Sep 19 Meeting Topics
Instantaneous Rates of Change: The Derivative (Book Section 2.1)
Concepts from Fri Sep 16.
Definition of the Derivative
- Words: the derivative of \(f(x)\)
- Symbol: \(f'(x)\)
- Meaning: \(f'(x) = \lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}\)
Definition of the Tangent Line
- Words: the line tangent to the graph of \(f(x)\) at \(x=a\)
- Meaning: the line that has these two properties:
- The line contains the point \((a,f(a))\).
- The line has slope \(m=f'(a)\).
The Point Slope Form of the Equation of a Line
If a line that has these two properties:
- The line contains the point \((a,b)\).
- the line has slope \((m\).
The Point Slope Form of the Equation of the Tangent Line
Since the tangent line that has these two properties:
- The line contains the point \((a,f(a))\).
- the line has slope \(m=f'(a)\).
New Concept: the Normal Line.
Definition of the Normal Line
- Words: the line normal to the graph of \(f(x)\) at \(x=a\)
- Meaning: the line that has these two properties:
- The line contains the point \((a,f(a))\).
- The line is perpendicular to the line that is tangent to the graph of \(f(x)\) at \(x=a\).
- Remark: By this definition, realize that if the tangent line has slope \(m=f'(a)\), where \(f'(a) \neq 0\), then the normal line will have slope \(m=-\frac{1}{f'(a)}\). But also realize that if the tangent line has slope \(m=f'(a)\), where \(f'(a) = 0\), then this means that the tangent line is horizontal. That will mean that the normal line will be vertical. Remember that vertical lines have undefined slope. One can still write a line equation for a vertical line. But it is in the form \(x=a\). That is, it is not in slope intercept form.
Class Presentations Involving Tangent Lines and Normal Lines for Mon Sep 19
Colin Sorge CP1 Let \(f(x)\) be the following function.
$$f(x)=5x-11$$In a previous presentation, a student found the derivative, \(f'(x)\), using the Definition of the Derivative. That is, they computed the following:
$$f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$$Their result was
$$f'(x)=5$$Using that result,
- Find the slope of the line tangent to the graph of \(f(x)\) at \(x=2\).
- Find the equation of the line tangent to the graph of \(f(x)\) at \(x=2\).
- Find the slope of the line normal to the graph of \(f(x)\) at \(x=2\).
- Find the equation of the line normal to the graph of \(f(x)\) at \(x=2\).
- Illustrate your results by drawing a graph of \(f(x)\) along with the tangent and normal lines.
- Make your graph large and neat. (You are welcome to use a graphing utility such as Desmos.)
- Label important points (such as axis intercepts and the point of tangency) with their \((x,y)\) coordinates.
- Label the curve for \(f(x)\) with its equation.
- Label the tangent line with its line equation.
- Label the normal line with its line equation.
Bilal Tahir CP1 Let \(f(x)\) be the following function.
$$f(x)=5x^2-11x+13$$In a previous presentation, a student found the derivative, \(f'(x)\), using the Definition of the Derivative. That is, they computed the following:
$$f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$$Their result was
$$f'(x)=10x-11$$Using that result,
- Find the slope of the line tangent to the graph of \(f(x)\) at \(x=2\).
- Find the equation of the line tangent to the graph of \(f(x)\) at \(x=2\).
- Find the slope of the line normal to the graph of \(f(x)\) at \(x=2\).
- Find the equation of the line normal to the graph of \(f(x)\) at \(x=2\).
- Illustrate your results by drawing a graph of \(f(x)\) along with the tangent and normal lines.
- Make your graph large and neat. (You are welcome to use a graphing utility such as Desmos.)
- Label important points (such as axis intercepts and the point of tangency) with their \((x,y)\) coordinates.
- Label the curve for \(f(x)\) with its equation.
- Label the tangent line with its line equation.
- Label the normal line with its line equation.
Paul Thorp CP1 Let \(f(x)\) be the following function.
$$f(x)=\frac{1}{x+7}$$In a previous presentation, a student found the derivative, \(f'(x)\), using the Definition of the Derivative. That is, they computed the following:
$$f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$$Their result was
$$f'(x)=-\frac{1}{(x+7)^2}$$Using that result,
- Find the slope of the line tangent to the graph of \(f(x)\) at \(x=2\).
- Find the equation of the line tangent to the graph of \(f(x)\) at \(x=2\).
- Find the slope of the line normal to the graph of \(f(x)\) at \(x=2\).
- Find the equation of the line normal to the graph of \(f(x)\) at \(x=2\).
- Illustrate your results by drawing a graph of \(f(x)\) along with the tangent and normal lines.
- Make your graph large and neat. (You are welcome to use a graphing utility such as Desmos.)
- Label important points (such as axis intercepts and the point of tangency) with their \((x,y)\) coordinates.
- Label the curve for \(f(x)\) with its equation.
- Label the tangent line with its line equation.
- Label the normal line with its line equation.
Tue Sep 20 Meeting Topics
Topic: Group Works About Interpretations Of The Derivative (Book Section 2.2)
- GW07: Representations of Slopes, Tue Sep 20
- GW08: Finding Derivatives Graphically Using a Ruler, Tue Sep 20
- GW09: Finding Derivatives Graphically Using a Ruler, Tue Sep 20
- GW10: Which is the Function; Which is the Derivative?, Tue Sep 20
Wed Sep 21 Meeting Topics
Interpretations of the Derivative (Book Section 2.2) (#1-18)
Class Presentations for Wed Sep 21
Three presentations that were originally assigned for Mon Sep 19.
Sara Weller CP1 Let \(f(x)\) be the following function.
$$f(x)=\sin (x)$$In book Example 2.1.19 the the authors computed the derivative, \(f'(x)\), using the Definition of the Derivative. That is, they computed the following:
$$f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$$Their result was
$$f'(x)=\cos(x)$$Using that result,
- Find the slope of the line tangent to the graph of \(f(x)\) at \(x=\pi\).
- Find the equation of the line tangent to the graph of \(f(x)\) at \(x=\pi\).
- Find the slope of the line normal to the graph of \(f(x)\) at \(x=\pi\).
- Find the equation of the line normal to the graph of \(f(x)\) at \(x=\pi\).
- Illustrate your results by drawing a graph of \(f(x)\) along with the tangent and normal lines.
- Make your graph large and neat. (You are welcome to use a graphing utility such as Desmos.)
- Label important points (such as axis intercepts and the point of tangency) with their \((x,y)\) coordinates.
- Label the curve for \(f(x)\) with its equation.
- Label the tangent line with its line equation.
- Label the normal line with its line equation.
Emily Wilkerson CP1 Let \(f(x)\) be the following function.
$$f(x)=\sin (x)$$In book Example 2.1.19 the the authors computed the derivative, \(f'(x)\), using the Definition of the Derivative. That is, they computed the following:
$$f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$$Their result was
$$f'(x)=\cos(x)$$Using that result,
- Find the slope of the line tangent to the graph of \(f(x)\) at \(x=\frac{\pi}{2}\).
- Find the equation of the line tangent to the graph of \(f(x)\) at \(x=\frac{\pi}{2}\).
- Find the slope of the line normal to the graph of \(f(x)\) at \(x=\frac{\pi}{2}\).
- Find the equation of the line normal to the graph of \(f(x)\) at \(x=\frac{\pi}{2}\).
- Illustrate your results by drawing a graph of \(f(x)\) along with the tangent and normal lines.
- Make your graph large and neat. (You are welcome to use a graphing utility such as Desmos.)
- Label important points (such as axis intercepts and the point of tangency) with their \((x,y)\) coordinates.
- Label the curve for \(f(x)\) with its equation.
- Label the tangent line with its line equation.
- Label the normal line with its line equation.
Gavin Wolfe CP1 Let \(f(x)\) be the following function.
$$f(x)=\sin (x)$$In book Example 2.1.19 the the authors computed the derivative, \(f'(x)\), using the Definition of the Derivative. That is, they computed the following:
$$f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$$Their result was
$$f'(x)=\cos(x)$$Using that result,
- Find the slope of the line tangent to the graph of \(f(x)\) at \(x=\frac{\pi}{4}\).
- Find the equation of the line tangent to the graph of \(f(x)\) at \(x=\frac{\pi}{4}\).
- Find the slope of the line normal to the graph of \(f(x)\) at \(x=\frac{\pi}{4}\).
- Find the equation of the line normal to the graph of \(f(x)\) at \(x=\frac{\pi}{4}\).
- Illustrate your results by drawing a graph of \(f(x)\) along with the tangent and normal lines.
- Make your graph large and neat. (You are welcome to use a graphing utility such as Desmos.)
- Label important points (such as axis intercepts and the point of tangency) with their \((x,y)\) coordinates.
- Label the curve for \(f(x)\) with its equation.
- Label the tangent line with its line equation.
- Label the normal line with its line equation.
Quiz Q03 Covering Section 2.1
Wed Sep 21 Quiz Q03 Covering Section 2.1
Fri Sep 23 Meeting Topics
Section 2.3 Basic Differentiation Rules (#1-38)
Class Presentations for Fri Sep 23
Nana Asare CP2: Using Theorem 2.3.1 and Theorem 2.3.4, compute the derivative of the function $$g(x)=16x^2-4x^3+24x+28$$ Use, as a model, the author's un-numbered example that immediately follows Theorem 2.3.4.
Tyler Boldon CP2: Using Theorem 2.3.1 and Theorem 2.3.4, compute the derivative of the function $$g(t)=16t^3+\cos{(t)}+7\sin{(t)}$$ Use, as a model, the author's un-numbered example that immediately follows Theorem 2.3.4.
Ellie Bower CP2: Using Theorem 2.3.1 and Theorem 2.3.4, compute the derivative of the function $$f(x)=\ln{(4x^8)}$$ Hint: We don't have a rule for computing the derivative of any sort of logarithmic function except the most basic one, \(y=\ln{(x)}\). So you'll have to use rules of logarithms to rewrite \(f(x)\) into a form involving \(ln{(x)}\).
Andrew Champagne CP2: Using Theorem 2.3.1 and Theorem 2.3.4, compute the derivatives of the following two functions
- \( f(x) = \ln{(x)}+e^{(x)}+\cos{(x)} \)
- \( f(x) = \ln{(2)}+e^3+\cos{(\frac{\pi}{3}) }\)
Drew Conway CP2: Using Theorem 2.3.1 and Definition 2.3.8, compute the first four derivatives of the function \(g(x)=-5\sin{(x)}\).
Week 6 (Mon Sep 26 through Fri Sep 30)
Book Sections and (Homework Exercises)
- Section 2.4 The Product and Quotient Rules (1-14, 15-47odd)
- Section 2.5 The Chain Rule (1-6, 7-39odd, 41, 42)
Mon Sep 26 Meeting Topics
Section 2.4 The Product and Quotient Rules
Exercises: Section 2.4 #1 - 14, 15 - 47 odd
Class Presentations for Mon Sep 26
Mark B presented this example.
- Using Theorem 2.4.1 Product Rule and theorems from Section 2.3, compute the derivative of the function $$f(x)=x^8\cos{(x)}$$
- Evaluate the derivative at \(x=\pi\). That is, find \(f'(\pi)\).
Carly Doros Presentation #2
- Using Theorem 2.4.1 Product Rule and theorems from Section 2.3, compute the derivative of the function $$f(x)=x^3\ln{(x)}$$ Simplify your answer.
- Evaluate the derivative at \(x=1\). That is, find \(f'(1)\). Give an exact, simplified answer.
- Evaluate the derivative at \(x=e\). That is, find \(f'(e)\). Give an exact, simplified answer.
Amy Evers Presentation #2
- Using Theorem 2.4.1 Product Rule and theorems from Section 2.3, compute the derivative of the function $$f(x)=\left(x^3+5x^2+7x+11\right)e^{(x)}$$
- Evaluate the derivative at \(x=0\). That is, find \(f'(0)\). Give an exact, simplified answer.
- Evaluate the derivative at \(x=1\). That is, find \(f'(1)\). Give an exact, simplified answer.
Paul Gbadebo Presentation #2
- Using Theorem 2.4.8 Quotient Rule and theorems from Section 2.3, compute the derivative of the function $$f(x)=\frac{x^2+3x+5}{x+2}$$
- Evaluate the derivative at \(x=1\). That is, find \(f'(1)\). Give an exact, simplified answer.
Dalana Goddard Presentation #2 Finding a Derivative Two Ways $$f(x)=\frac{x^2+3x+5}{x}$$
- Using Theorem 2.4.8 Quotient Rule, compute \(f'(x)\).
- Start over. This time, start by simplifying \(f(x)\) through division. Rewrite \(f(x)\) in power function form. That is, write \(f(x)\) in the form $$f(x)=ax^p+bx^q+cx^r$$ where \(a,b,c\) are constants and \(x^p,x^q,x^r\) are power functions. Then find \(f'(x)\) using the simpler derivative rules (the Sum and Constant Multiple Rule, the Power Rule, and the Constant Function Rule).
Tue Sep 27 Meeting Topics
Section 2.4 The Chain Rule
Exercises: Section 2.5: #1-6, 7-39odd, 41, 42
Discussed nested functions. That is, functions of the form
$$f(x)=outer\left(inner(x)\right)$$Question: How to find the derivative of such a function?
Answer: Theorem 2.5.3 The Chain Rule
$$\frac{d}{dx}outer\left(inner(x)\right) = outer’\left(inner(x)\right) \cdot inner’(x)$$Examples
[Example 1]: For \(f(x)=\left(\cos{(x)}\right)^2\), find \(f’(x)\).
[Example 2]: For \(f(x)=\cos{\left(x^2\right)}\), find \(f’(x)\).
[Example 3: For \(f(x)=\cos{\left(\ln{(x)}\right)}\), find \(f’(x)\).
[Example 4]: For \(f(x)=\ln\left(\cos{(x)}\right)\), find \(f’(x)\).
Discuss Basic Derivative Rules from Section 2.3
Discuss these Derivative Rules:
- Constant Function Rule: If \(f(x)=c\) then \(f’(x)=0\).
- Sine Function Rule: If \(f(x)=\sin{(x)}\) then \(f’(x)=\cos{(x)}\).
- Exponential Function Rule: If \(f(x)=e^{(x)}\) then \(f’(x)=e^{(x)}\).
- Logarithm Function Rule: If \(f(x)=\ln{(x)}\) then \(f’(x)=\frac{1}{x}\).
For each Derivative Rule, do an construction similar to those done in Group Works GW08 and GW09, Finding Derivatives Graphically Using a Ruler.
- Draw basic graph of \(f(x)\).
- Pin some tangent lines to the graph of \(f(x)\).
- Estimate the slopes of those tangent lines.
- Use the slope date to draw a crude graph of \(f’(x)\).
- Observe that the drawn graph of \(f’(x)\) agrees with the function \(f’(x)\) given by the Derivative Rule.
Wed Sep 28 Meeting Topics
Section 2.5 The Chain Rule
Exercises: Section 2.5: #1 - 6,1 - 39 odd, 41, 42
More Examples involving the Chain Rule
$$\frac{d}{dx}outer\left(inner(x)\right) = outer’\left(inner(x)\right) \cdot inner’(x)$$Class Presentations for Wed Sep 28
Nicole Grant Presentation #2 For the following function $$f(x)=\left(x^2-4x+3\right)^3$$
- Find \(f'(x)\) using Theorem 2.5.3 the Chain Rule.
- Find the \(x\) coordinates of all points on the graph of \(f(x)\) that have horizontal tangent lines.
(Hint: Remember that a horizontal line has slope \(m=0\). Also remember that the slope of the line tangent to the graph of \(f(x)\) at \(x=a\) is \(m=f'(a)\). So you should look for all values of \(x\) that cause \(f'(x)=0\). In other words, set \(f'(x)=0\) and solve for \(x)\).
Evan Green Presentation #2 For the following function $$f(x)=e^{\left(x^2-6x+5\right)}$$
- Find \(f'(x)\) using Theorem 2.5.3 the Chain Rule.
- Evaluate the derivative at \(x=0\). That is, find \(f'(0)\).
- Find the slope of the line tangent to the graph of \(f(x)\) at \(x=0\).
- Find the \(x\) coordinates of all points on the graph of \(f(x)\) that have horizontal tangent lines.
(Hint: Remember that a horizontal line has slope \(m=0\). Also remember that the slope of the line tangent to the graph of \(f(x)\) at \(x=a\) is \(m=f'(a)\). So you should look for all values of \(x\) that cause \(f'(x)=0\). In other words, set \(f'(x)=0\) and solve for \(x)\).
Mark Discussed the Zero Product Property, and how it is used in solving the equation
$$e^{\left(x^2-6x+5\right)}\cdot (2x-6)=0$$Kierston Harper Presentation #2 For the following function $$f(x)=\sin{(2x)}$$
- Find \(f'(x)\) using Theorem 2.5.3 the Chain Rule.
- Evaluate the derivative at \(x=0\). That is, find \(f'(0)\).
- Find the slope of the line tangent to the graph of \(f(x)\) at \(x=0\).
- Find the equation of the line tangent to the graph of \(f(x)\) at \(x=0\).
Wed Sep 28 Quiz Q04 Covering Sections 2.3 and 2.4
Quiz Q04 Information
- 20 Minutes at the end of class
- No Calculators
- Six Problems
- Compute a derivative using Section 2.3 Derivative Rules (Practice: 2.3 # 11-25 odd)
- Compute a derivative using Section 2.3 Derivative Rules (Practice: 2.3 # 11-25 odd)
- Compute a derivative using Section 2.3 Derivative Rule (Practice: 2.3 # 11-25 odd)
- Compute a derivative using the Product Rule (Section 2.4 Concept) (Practice: 2.4 # 15 - 36 odd)
- Compute a derivative using the Quotient Rule (Section 2.4 Concept) (Practice: 2.4 # 15 - 36 odd)
- A problem similar to 2.4 # 11 - 14. Given a function \(f(x)\) presented as a quotient,
- Use the Quotient Rule to find \(f'(x)\).
- Start over. Simplify \(f(x)\) to a form that is not a quotient, and then use simpler derivative rules to find \(f'(x)\).
Fri Sep 30 Fall Break: Stay Home and Study Math!
Week 7 (Mon Oct 3 through Fri Oct 7)
Book Sections and (Homework Exercises)
- Section 2.6 Implicit Differentiation (1-4, 5-25odd, 26, 27-41odd)
Mon Oct 3 Meeting Topics
Section 2.6 Implicit Differentiation
Exercises: Section 2.6: #1-4, 5-25odd, 26, 27-41odd
Topic 1: Some Derivative Calculations Using Old Rules (Sections 2.3, 2.4, 2.5)
Mark B will do an example, and we’ll have two presentations.
Topic 2: The Power Rule for Derivatives, Valid for All Real Number Exponents
In our book, the Power Rule For Derivatives $$\frac{d}{dx}x^n=nx^{n-1}$$ is rolled out gradually.
- In Book Section 2.3, the Power Rule is presented (without proof) for positive integer exponents. That is, \(n \in \mathbb{Z}\) and \( n \gt 0\).
- In Book Section 2.4, the authors use the Quotient Rule to prove that the Power Rule is proved to hold for all integer exponents, including positive, negative and zero. That is, \(n \in \mathbb{Z}\).
- It is possible to use the Chain Rule (from Book Section 2.5) to show that the Power Rule actually holds for all rational number exponents. That is, \(n \in \mathbb{Q}\). The authors do not do this in the book.
- In Book Section 2.6, the authors use Implicit Differentiation prove that the Power Rule holds for all rational number exponents. That is, \(n \in \mathbb{Q}\). Since the method of Implicit Differentiation is basically a variation on the Chain Rule, the author’s proof in Book Section 2.6 looks similar to what could have been done (but wasn’t done) in Section 2.5.
- Finally, in Book Section 2.6, the authors state (but do not prove) the most general result: The Power Rule holds for all real number exponents. That is, \(n \in \mathbb{R}\).
So far in our class examples and presentations, we have only found derivatives of power functions that have positive integer exponents. We’ll have four presentations that involve finding the derivatives of functions that have more general exponents.
Class Presentations for Mon Oct 3
Lauren Hartel CP2 (We didn’t get to this last Wednesday.):
For the following function
$$f(x)=\ln{\left(x^2-4x+3\right)}$$
- Find \(f'(x)\) using Theorem 2.5.3 the Chain Rule.
- Find \(f”(x)\).
Carlotta Dattilo CP2: For the function $$f(x)=e^{(x)}+x^e+x^{1.9}+e^{1.9}$$
- Find \(f’(x)\)
- Find \(f'(1)\)
Tim Jaskiewicz CP2: For the function
$$f(x)=\sqrt[3]{x}+x^{2/3}$$- Find \(f’(x)\). Write your final answer in positive exponent form. That is, eliminate all negative exponents.
- Find \(f'(8)\)
Hints for (a):
- Remember that \(\sqrt[n]{a}=a^{1/n}\).
- Remember that \(a^{-b}=\frac{1}{a^b}\).
Hint for (b): Remember that \(a^{b/c}=a^{(1/c)\cdot b} =\left(a^{(1/c)}\right)^b\).
Olivia Keener CP2: For the function
$$f(x)=\sqrt{x^2-6x+16}$$- Find \(f’(x)\) using the Chain Rule. Write your final answer in positive exponent form. That is, eliminate all negative exponents.
- Find \(f'(0)\)
- Find the \(x\) coordinates of all points on the graph of \(f(x)\) that have horizontal tangent lines.
Hints for (a):
- For the outer function, use \(outer( \ \ ) = \sqrt{( \ \ )} = ( \ \ )^{1/2}\).
- Remember that \(a^{-b}=\frac{1}{a^b}\).
Hint for (c): Remember that a horizontal line has slope \(m=0\). Also remember that the slope of the line tangent to the graph of \(f(x)\) at \(x=a\) is \(m=f'(a)\). So you should look for all values of \(x\) that cause \(f'(x)=0\). In other words, set \(f'(x)=0\) and solve for \(x)\).
Austin Kiggins CP2: For the function $$f(x)=\frac{5x+7}{\sqrt{x}}$$ the goal is to find \(f’(x)\). This could be done using the Quotient Rule, but that would be really hard. A better approach is to first rewrite \(f(x)\), putting it into a form where simpler derivative rules can be used.
- Rewrite \(f(x)\) in power function form. That is, rewrite it in the form $$f(x)=ax^b+cx^d$$ This form is a sum of terms where each term is a product of a constant and a power function. That’s why it is called power function form.
- Now find \(f’(x)\). Start by using the simpler derivative rules from Section 2.3. That is, use the Sum Rule and the Constant Multiple Rule. Then use the Power Rule. Write your final answer in positive exponent form. That is, eliminate all negative exponents.
- Remember that \(\sqrt{a}=a^{1/2}\).
- Remember that \(a^{-b}=\frac{1}{a^b}\).
Kelly Koenig CP2 (Old Stuff): Show how the Theorem 2.4.8 the Quotient Rule can be used to find the derivative of \(f(x)=\tan{(x)}\).
Tue Oct 4 Meeting Topics
Section 2.6 Implicit Differentiation
Exercises: Section 2.6: #1-4, 5-25odd, 26, 27-41odd
Topic 1: The Method of Implicit Differentiation
(Used for finding \(\frac{dy}{dx}\) when \(x\) and \(y\) are related by an equation that is not solved for \(y\).)
Starting with: An equation involving \(x\) and \(y\).
Step 1: Replace all \(y\) with the symbol \(y(x)\), indicating that \(y\) is a function of \(x\) . Add parentheses, if necessary, to clarify notation and order of operations. The result will be a new equation involving \(x\) and \(y(x)\).
Step 2: Take derivative of left and right sides of the equation from Step 1 with respect to \(x\) . That is, take \(\frac{d}{dx}\) of both sides. This will require the Chain Rule. Note that when the inner function is \(inner(x)=y(x)\), you should just leave the \(inner'(x)\) in the form \(inner’(x)=\frac{dy(x)}{dx}\). The result will be a new equation involving \(x\) and \(y(x)\) and \(\frac{dy(x)}{dx}\).
Step 3: In the equation from Step 2, replace all \(y(x)\) with just \(y\). The result will be a new equation involving \(x\) and \(y\) and \(\frac{dy}{dx}\).
Step 4: Solve the equation from Step 3 for \(\frac{dy}{dx}\). The result will be a new equation of the form $$\frac{dy}{dx}=\text{expression involving }x\text{ and }y$$
Mark B will present two examples involving the method of Implicit Differentiation.
Two students will do presentations involving .
Class Presentations for Tue Oct 4
Student #1 Presentation CP2
Suppose that \(3x^2+5xy+7y^2=11\). Use Implicit Differentiation to find \(\frac{dy}{dx}\).
Student #2 Presentation CP2
Suppose that \(x^2+y^2=1\).
- Use Implicit Differentiation to find \(\frac{dy}{dx}\).
- Find the slope of the line tangent to the graph of \(x^2+y^2=1\) at the point \((x,y)=(-\frac{\sqrt3}{2},\frac{1}{2})\).
- Find the equation of the line tangent to the graph of \(x^2+y^2=1\) at the point \((x,y)=(-\frac{\sqrt3}{2},\frac{1}{2})\).
- Graph the equation \(x^2+y^2=1\), along with the tangent line that you found in (c). Make your graph large and neat, and put \((x,y)\) coordinates on all important locations.
Student Number assignments:
- In Section 173 (Tue 9:30)
- Ben Oldiges is Student #1
- Sara Weller is Student #2
- In Section 174 (Tue 11:00)
- Bilal Tahir is Student #1
- Gavin Wolfe is Student #2
- In Section 175 (Tue 2:00)
- Jonah Lewis is Student #1
- Dylan Pohovey is Student #2
- In Section 176 (Tue 3:30)
- Alan Romero Herrera is Student #1
- Reggie Shaffer is Student #2
Group Work: GW11: Rewrite Function, then Find the Derivative.
Wed Oct 5 Meeting Topics
Topic 1: Logarithmic Differentiation (Section 2.6)
We know how to find derivatives of two kinds of functions that contain exponents.
- \(x^n\) is a power function, so we use the Power Rule to find its derivative. That is, \(\frac{d}{dx}x^n=nx^{n-1}\).
- \(a^x\) is an exponential function, so we use the General Exponential Function Rule to find its derivative. That is, \(\frac{d}{dx}a^n=a^\cdot \ln{(a)}\).
What about the function \(x^x\)? It is neither a power function nor an exponential function. How do we find its derivative?
Mark B will explain the technique of Logarithmic Differentiation.
Topic 2: Leftover from Sections 2.2 and 2.3: Approximation with the Derivative
Class Presentations for Wed Oct 5
Presentations about Approximating Using the Tangent Line
Colin Sorge CP2: For the function \(f(x)=e^{(x)}\),
- Find \(f(0)\).
- Use a calculator or computer to get a decimal approximation for the value of \(f(0.1)\), rounded to 5 decimal places.
- Find the slope of the line tangent to the graph of \(f(x)\) at \(x=0\).
- Find the equation of the line tangent to the graph of \(f(x)\) at \(x=0\). Present your result in slope intercept form.
- Without using a calculator or computer, find the \(y\) value on the tangent line from (d) at \(x=0.1\).
- Compare your results of (b) and (e).
Paul Thorp CP2: (Use units of radians in this problem.) For the function \(f(x)=\sin{(x)}\),
- Find \(f(0)\).
- Use a calculator or computer to get a decimal approximation for the value of \(f(0.1)\), rounded to 5 decimal places.
- Find the slope of the line tangent to the graph of \(f(x)\) at \(x=0\).
- Find the equation of the line tangent to the graph of \(f(x)\) at \(x=0\). Present your result in slope intercept form.
- Without using a calculator or computer, find the \(y\) value on the tangent line from (d) at \(x=0.1\).
- Compare your results of (b) and (e).
Emily Wilkerson CP2: For the function \(f(x)=\sqrt x\),
- Find \(f(4)\).
- Use a calculator or computer to get a decimal approximation for the value of \(f(4.1)\), rounded to 5 decimal places.
- Find the slope of the line tangent to the graph of \(f(x)\) at \(x=4\).
- Find the equation of the line tangent to the graph of \(f(x)\) at \(x=4\). Present your result in slope intercept form.
- Without using a calculator or computer, find the \(y\) value on the tangent line from (d) at \(x=4.1\).
- Compare your results of (b) and (e).
Fri Oct 7 Exam X2 Covering Chapter 2
Exam X2 Information
- The full duration of the class meeting
- No Calculators
- 8 problems, typeset on 4 pages, printed on front & back of 2 sheets of paper.
- Find one derivative using the Definition of the Derivative (not the Derivative Rules). Study 2.1#7-14
- Compute some derivatives using the Derivative Rules (not the Definition of the Derivative). Problems of this sort are found in Sections 2.3, 2.4, 2.5, 2.6.
- Compute some derivatives using the Derivative Rules (not the Definition of the Derivative). Problems of this sort are found in Sections 2.3, 2.4, 2.5, 2.6.
- Compute some derivatives using the Derivative Rules (not the Definition of the Derivative). Problems of this sort are found in Sections 2.3, 2.4, 2.5, 2.6.
- A problem like the problem on the 2nd page of Group Work GW11. Study that GW.
- A problem about slope of the tangent line and/or equation of the tangent line (but not involving Implicit Differentiation). Problems of this sort are found in Sections 2.3, 2.4, 2.5.
- A problem involving Implicit Differentiation. Problems of this sort are found in Section 2.6.
- A problem about approximating using the tangent line. (Problems of this sort are found in Sections 2.2 and 2.3 and in the Presentations for Wed Oct 5.)
Week 8 (Mon Oct 10 through Fri Oct 14)
Book Sections and (Homework Exercises)
- Section 3.1 Extreme Values (1-6, 7-25odd)
- Section 3.2 The Mean Value Theorem (1, 2, 3-20odd)
- Section 3.3 Increasing and Decreasing Functions (1-6, 7-23odd)
Mon Oct 10 Meeting Topics
Book Sections and (Homework Exercises): Section 3.1 Extreme Values (1-6, 7-25odd)
Discussed these topics from Section 3.1:
- Absolute Extrema (Absolute Max and Absolute Min)
- The Extreme Value Theorem
- Relative Extrema (Relative Max and Relative Min)
Students did Group Work GW12: The Extreme Value Theorem.
Tue Oct 11 Meeting Topics
Book Sections and (Homework Exercises): Section 3.1 Extreme Values (1-6, 7-25odd)
Discuss these topics from Section 3.1:
- Definition 3.1.11 Critical Numbers and Critical Points
- Theorem 3.1.12 Relative Extrema and Critical Points
- Key Idea 3.1.14 Finding Extrema on a Closed Interval (presentations are about this)
Class Presentations for Tue Oct 11
Student #1 Presentation CP3
- Find the extrema of \(f(x)=x \cdot e^{(x)}\) on the interval \([-2,2]\).
- Illustrate with a graph of \(f(x)\).
Student #2 Presentation CP3
- Find the extrema of \(f(x)=x^3-3x^2-9x-1\) on the interval \([-2,5]\).
- Illustrate with a graph of \(f(x)\).
Student Number assignments:
- In Section 173 (Tue 9:30)
- Nana Asare is Student #1
- Tyler Boldon is Student #2
- In Section 174 (Tue 11:00)
- Andrew Champgagne is Student #1
- Drew Conway is Student #2
- In Section 175 (Tue 2:00)
- Evan Green is Student #1
- Kierston Harper is Student #2
- In Section 176 (Tue 3:30)
- Carlotta Dattilo is Student #1
- Paul Gbadebo is Student #2
Discussed more examples of Finding Extrema on a Closed Interval.
Students did Group Work GW13: Finding Absolute Extrema on a Closed Interval.
Students did Group Work GW14: Comparing Two Solutions to an Absolute Extrema Problem.
Wed Oct 12 Meeting Topics
Book Sections and (Homework Exercises): 3.2 The Mean Value Theorem (1, 2, 3-20odd)
Reviewed these old concepts (from book Section 2.1)
- The Average Rate of Change, \(m=\frac{f(b)-f(a)}{b-a}\), which is the slope of a secant line on the graph of the function
- The Instantaneous Rate of Change, \(m=\lim_{h\rightarrow 0}\frac{f(c+h)-f(C)}{h}\), which is the slope of a secant line on the graph of the function
Discussed the Mean Value Theorem (from book Section 3.2)
Theorem 3.2.3 The Mean Value Theorem
Let \(f(x)\) be a continuous function on the closed interval \([a,b]\) and differentiable on the open interval \((a,b)\). There exists an \(x\)value, \(x=c\), such that $$f’(c)=\frac{f(b)-f(a)}{b-a}$$ That is, there is at least one \(x\) value, \(x=c\), in the interval \((a,b)\) such that the instantaneous rate of change of \(f(x)\) at \(x=c\) is equal to the average rate of change of \(f(x)\) on the interval \([a,b]\).
In terms of the graph, this meant that there is at least one \(x\) value, \(x=c\), in the interval \((a,b)\) such that the line tangent to the graph of \(f(x)\) at \(x=c\) has the same slope as the secant line that touches the graph of \(f(x)\) at \(x=a\) and \(x=b\).
Saw Four Examples Involving the Mean Value Theorem
- Tim Jaskiewicz CP3: (book exercise 3.2#12) Can the Mean Value Theorem be applied to the function \(f(x)=5x^x-6x+8\) on the interval \([0,5]\)? If so, find a number \(c\) in the interval \((0,5)\) that is guaranteed by the Mean Value Theorem.
- Olivia Keener CP3: (book exercise 3.2#14) Can the Mean Value Theorem be applied to the function \(f(x)=\sqrt{25-x}\) on the interval \([0,9]\)? If so, find a number \(c\) in the interval \((0,9)\) that is guaranteed by the Mean Value Theorem.
- Paul Thorp CP3: (book exercise 3.2#16) Can the Mean Value Theorem be applied to the function \(f(x)=\ln{(x)}\) on the interval \([1,5]\)? If so, find a number \(c\) in the interval \((1,5)\) that is guaranteed by the Mean Value Theorem.
- Mark B: For the function \(f(x)=\frac{1}{x}\) on the interval \([-1,1]\), it does not seem possible to find a number \(c\) in the interval \((-1,1)\) such that $$f’(c)=\frac{f(1)-f(-1)}{1-(-1)}$$ Why not?!?
Fri Oct 14 Meeting Topics
Book Sections and (Homework Exercises): Section 3.3 Increasing and Decreasing Functions (1-6, 7-23odd)
Discussed these topics from Section 3.3:
- Definition 3.3.2 Definition of Increasing and Decreasing Functions
- Theorem 3.3.4 Test for Increasing/Decreasing
Discussed method of making a Sign Chart to determine the sign behavior of a function.
[Increasing/Decreasing Example] For the function $$f(x)=x^4-6x^2+5$$ find the intervals where \(f(x)\) is increasing and the intervals where \(f(x)\) is decreasing.
Note that this was the same function that was studied on Tue Oct 11, in Group Work GW13: Finding Absolute Extrema on a Closed Interval. In that Group Work, students found that $$f’(x)=4x^3-6x=4x(x^2-3)=4x(x+\sqrt{3})(x-\sqrt{3})$$ The critical numbers for \(f(x)\) are \(x=-\sqrt{3},0,\sqrt{3}\).
To solve the problem in the current [Example], a sign chart was constructed for \(f’(x)\) to determine its sign behavior. Then Theorem 3.3.4 Test for Increasing/Decreasing was used to make the following conclusions:
- \(f(x)\) is increasing on the intervals \([-\sqrt{3},0]\) and \([\sqrt{3},\infty)\) because \(f’(x)\) is positive there.
- \(f(x)\) is decreasing on the intervals \((-\infty,-\sqrt{3}]\) and \([0,\sqrt{3}]\) because \(f’(x)\) is negative there.
Quiz Q5 on Friday Oct 14 covering Sections 3.1 and 3.2
Week 9 (Mon Oct 17 through Fri Oct 21)
Book Sections and (Homework Exercises)
- Section 3.3 Increasing and Decreasing Functions (1-6, 7-23odd)
- Section 3.4 Concavity and the Second Derivative (1-4, 5-56odd)
- Section 3.5 Curve Sketching (1-5, 6-25odd, 26-28)
Mon Oct 17 Meeting Topics
Book Sections and (Homework Exercises): Section 3.3 Increasing and Decreasing Functions (1-6, 7-23odd)
Reviewed past topics from Section 3.1 and 3.3 that were discussed last week
- Definition 3.1.1 Extreme Values (absolute max and absolute min)
- Theorem 3.1.3 The Extreme Value Theorem If \(f(x)\) is a continuous function defined on a closed interval \(I=[a,b]\), then \(f(x)\) has both an absolute max and an absolute min on the interval \(I\).
- Definition 3.1.6 Relative Max and Relative Min
- Definition 3.1.11 Critical Numbers and Critical Points
- Theorem 3.1.11 Critical Numbers and Critical Points Relative extrema can only occur at \(x\) values that are critical numbers.
- Fact Absolute extrema can only occur at \(x\) values that are endpoint of the domain or critical numbers.
- Key Idea 3.1.4 Method for finding absolute extrema for a function \(f(x)\) that is continuous on a closed interval.
- Definition 3.3.2 Definition of Increasing and Decreasing Functions
- Theorem 3.3.4 Test for Increasing/Decreasing
Discussed new topic from Section 3.3:
- Theorem 3.3.10 First Derivative Test
Amy Evers Presentation CP3: Find the critical numbers for the function \(f(x)=xe^{(-x)}\).
[Example 1] (done by Mark B) Find the relative extrema for the function \(f(x)=xe^{(-x)}\).
Ben Oldiges Presentation CP3: Find the critical numbers for the function \(f(x)=\frac{1}{x^2}\).
[Example 2] (done by Mark B) Find the relative extrema for the function \(f(x)=\frac{1}{x^2}\).
Tue Oct 18 Meeting Topics
Book Sections and (Homework Exercises): Section 3.3 Increasing and Decreasing Functions (1-6, 7-23odd)
Discussed Partition Numbers and Critical Numbers
A partition number for a function \(g(x)\) is an \(x\) value where \(g(x)=0\) or \(g\) is discontinuous.
Remark: A function \(g(x)\) can only change sign at its partition numbers.
A critical number for a function \(f(x)\) is an \(x\) value \(x=c\) that has these two properties:
- \(x=c\) is a partition number for \(f'(x)\). That is, \(f'(c)=0\) or \(f'\) is discontinuous at \(x=c\).
- \(f\) is continuous at \(x=c\).
Class Presentations for Tue Oct 18
Student #1 Presentation CP3 Find the critical numbers for the function $$f(x)=x+\frac{4}{x}$$
Student #2 Presentation CP3 Find the critical numbers for the function $$f(x)=\frac{x}{x^2+9}$$
Student Number assignments:
- In Section 173 (Tue 9:30)
- Sara Weller is Student #1
- Ellie Bower is Student #2
- In Section 174 (Tue 11:00)
- Nicole Grant is Student #1
- Bilal Tahir is Student #2
- In Section 175 (Tue 2:00)
- Austin Kiggins is Student #1
- Jonah Lewis is Student #2
- In Section 176 (Tue 3:30)
- Carlotta Dattilo is Student #1
- Paul Gbadebo is Student #2
Students did three Group Works.
- GW15: Analyzing a Polynomial, Tue Oct 18
- GW16: Analyzing a Rational Function with a Vertical Asymptote, Tue Oct 18
- GW17: Analyzing a Rational Function with a Horizontal Asymptote, Tue Oct 18
Wed Oct 19 Meeting Topics
Book Sections and (Homework Exercises)
- Section 3.4 Concavity and the Second Derivative (1-4, 5-56odd)
- Section 3.5 Curve Sketching (1-5, 6-25odd, 26-28)
Discussed Section 3.4 Concavity and the Second Derivative
Discussed Section 3.5 Curve Sketching
Students did a Group Work.
- GW18: Using Given Information to Sketch a Graph, Wed Oct 19
Fri Oct 21 Meeting Topics
Book Sections and (Homework Exercises): Section 3.5 Curve Sketching (1-5, 6-25odd, 26-28)
Class Presentations for Fri Oct 21
Dalana Goddard Presentation CP3: Given the following in formation about \(f,f’,f”\):
- \(f(x)\)is continuous for all x
- \(f(7)=10\)
- \(f’(x)\) is positive on the interval \((-\infty,2)\).
- \(f’(2)=0\)
- \(f’(x)\) is negative on the interval \((2,12)\).
- \(f’(12)=0\)
- \(f’(x)\) is positive on the interval \((12,\infty)\).
- \(f’’(x)\) is negative on the interval \((-\infty,7)\).
- \(f’’(7)=0\)
- \(f’’(x)\) is positive on the interval \((7,\infty)\).
Lauren Hartel Presentation CP3 The graph of a function \(f(x)\) is given without gridlines and without coordinate axes.
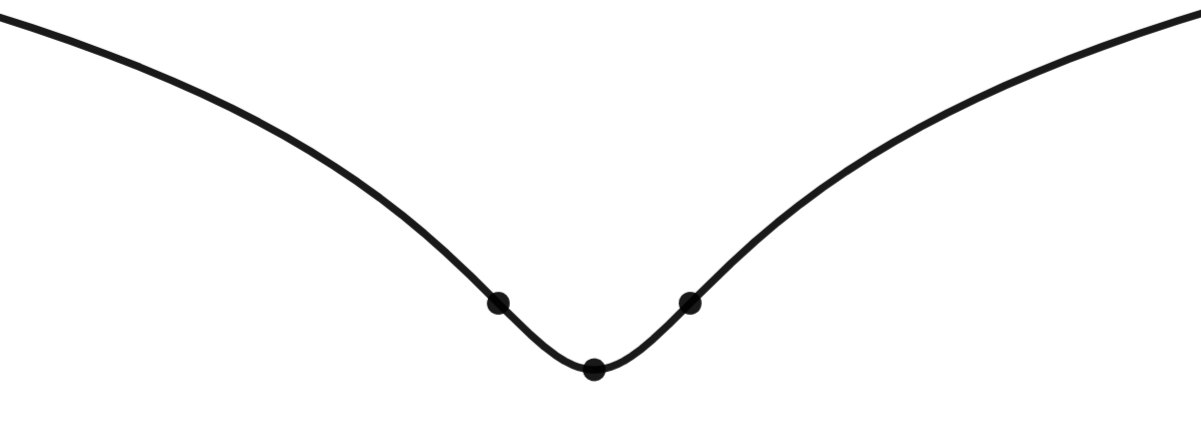
The formula for \(f(x)\) is not given, but the formulas for its first and second derivatives are
$$\begin{eqnarray} f’(x) &=& \frac{x}{x^2+1} \\ f”(x) &=& -\frac{2(x^2-1)}{(x^2+1)^2}=-\frac{2(x+1)(x-1)}{(x^2+1)^2} \end{eqnarray}$$- It looks like there is a relative min on the graph of \(f(x)\). What is the \(x\) coordinate of that point? Explain how you know.
- It looks like there is are two inflection points on the graph of \(f(x)\). What are the \(x\) coordinates of those point? Explain how you know.
Quiz Q6 on Friday Oct 21 covering Section 3.3
Week 10 (Mon Oct 24 through Fri Oct 28)
Book Sections and (Homework Exercises)
- Section 4.1 Newton's Method (3, 5, 7, 17)
- Section 4.2 Related Rates (3-15odd)
Mon Oct 24 Meeting Topics
Curve Sketching (Section 3.5)
Mark Did Some more examples involving curve sketching.
Class Presentations for Mon Oct 24, having to do with Curve Sketching
Carly Doros Presentation CP3: The derivative of \(f(x) = e^{(-x^2)}\) is $$f'(x)= -2xe^{(-x^2)}$$
- Show how \(f'(x)\) is obtained.
- Make a sign chart for \(f'(x)\).
- Using your sign chart for \(f'(x)\), determine the intervals where \(f(x)\) is increasing and decreasing. Present your answer in interval notation.
- Determine the \(x\) coordinates of all relative extrema of \(f(x)\).
- Find the corresponding \(y\) coordinates of the relative extrema.
Dylan Pohovey Presentation CP3: The second derivative of \(f(x) = e^{(-x^2)}\) is $$f''(x)= (4x^2-2)e^{(-x^2)}$$
- Show how \(f''(x)\) is obtained.
- Make a sign chart for \(f''(x)\). It will be helpful to note that \(f''(x)\) can be factored as $$f''(x)= (4x^2-2)e^{(-x^2)} = 4(x^2-\frac{1}{2})e^{(-x^2)} = 4(x+\frac{1}{\sqrt{2}})(x-\frac{1}{\sqrt{2}})e^{(-x^2)}$$
- Using your sign chart for \(f'(x)\), determine the intervals where \(f(x)\) is concave up and concave down. Present your answer in interval notation.
- Determine the \(x\) coordinates of all inflection points of \(f(x)\).
- Find the corresponding \(y\) coordinates of the inflection points.
Newton's Method (Section 4.1) (Suggested Exercises 4.1# 3, 5, 7, 17)
Students worked on Group Work GW19: The Idea Behind Newton’s Method
Then Mark discussed Newton’s Method
Tue Oct 25 Meeting Topics
Topic for Today: Analyzing a function and then graphing it, using the Graphing Strategy
(Concepts from Section 3.5)
We will be discussing the following function:
$$f(x)=-x^4+4x^3$$Refer to the Reference R05: Graphing Strategy, handed out in class on Wed Oct 19.
First Presentation, presented by these students:
- In Section 173 (Tue 9:30), Nana Asare CP4
- In Section 174 (Tue 11:00), Gavin Wolfe CP3
- In Section 175 (Tue 2:00), Kierston Harper CP4
- In Section 176 (Tue 3:30), Kelly Koenig CP3
Second Presentation, presented by these students:
- In Section 173 (Tue 9:30), Tyler Boldon CP4
- In Section 174 (Tue 11:00), Drew Conway CP4
- In Section 175 (Tue 2:00), Evan Green CP4
- In Section 176 (Tue 3:30), Reggie Shaffer CP3
Groups: Complete GW20: Using the Graphing Strategy to Analyze and Graph a Polynomial
Wed Oct 26 Meeting Topics
Topic for Today: Newton's Method (Section 4.1) (Suggested Exercises 4.1# 3, 5, 7, 17)
Students finished the Group Work that was begun on Monday: GW19: The Idea Behind Newton’s Method.
Mark Discussed Newton’s Method.
Students worked on Group Work GW21: Newton’s Method
Class Presentations for Wed Oct 26, having to do with Newton’s Method
Ellie Bower CP4: In the Group Work GW21: Newton’s Method, students used Newton’s Method to find an approximate value for the root of the function $$f(x)=x^3-x^2-1$$ In the group work, they were given an initial approximation \(x_0=1\), and they used Newton’s Method to find \(x_1\) and \(x_2\).
Your job is to find a web site that has a Newton’s Method Calculator. There are lots of them. Using the function \(f(x)=x^3-x^2-1\) and the initial approximation \(x_0=1\), show the web site calculator results for the first \(10\) or so steps. That is, display \(x_0\) through roughly \(x_{10}\). Comment on whether the results that the calculator displays for \(x_1\) and \(x_2\) match the values obtained by your group.
Andrew Champagne CP4: In the Group Work GW21: Newton’s Method, students used Newton’s Method to find an approximate value for the root of the function $$f(x)=x^3-x^2-1$$ Show what happens when you ask Wolfram Alpha to find a root of \(f(x)\). That is, ask Wolfram Alpha to solve the equation $$f(x)=0$$ Show the result in both the exact form and the decimal approximation (the approximate form).
Fri Oct 28 Meeting Topic: Section 4.2 Related Rates (3-15odd)
Topic for Today: Related Rates (Section 4.2)
Quiz Q07 on Friday Oct 28
The Quiz will be over Newton’s Method (from Section 4.1). The quiz will be one problem, with three questions that are similar to the questions in Group Work GW21: Newton’s Method. That is, a problem like this:
The goal is to use Newton’s Method to find an approximate value for a root of the function \(f(x)=\text{some function}\), using the initial approximation \(x_0=4\).
- Compute \(f’(x)\).
- Fill in a table that is a worksheet for finding the values of \(x_1\), \(x_2\), and \(x_3\). (similar to the table in GW21)
- A graph of \(f(x)\) is shown. Illustrate your results on this graph. (illustrations similar to the illustration in GW21)
To prepare for the quiz:
- Read your MATH 2301 class notes from Wed Oct 26 meeting.
- Review the Group Work GW21: Newton’s Method.
- Work the suggested exercises 4.1#3,5,7. These book exercises are written with calculators in mind. Go ahead and use your calculator for your studying. The quiz problem will be a simple polynomial function that you can analyze without a calculator.
Week 11 (Mon Oct 31 through Fri Nov 4)
Book Sections and (Homework Exercises)
- Section 4.3 Optimization (8, 9, 11, 12, 13, 15, 18)
- Section 4.4 Differentials (1-6, 7-13odd, 17-39odd)
- Section 5.1 Antiderivatives and Indefinite Integration (9-27odd, 28, 29, 31-39odd)
Tue Nov 1 Meeting
Topic for Today: Related Rates problems involving Right Triangles
(Concepts from Section 4.2)
First Presentation, presented by these students:
- In Section 173 (Tue 9:30), Amy Evers CP4
- In Section 174 (Tue 11:00), Carly Doros CP4
- In Section 175 (Tue 2:00), Austin Kiggins CP4
- In Section 176 (Tue 3:30), Paul Gbadebo CP4
Second Presentation, presented by these students:
- In Section 173 (Tue 9:30), Dalana Goddard CP4
- In Section 174 (Tue 11:00), Nicole Grant CP4
- In Section 175 (Tue 2:00), Dylan Pohovey CP4
- In Section 176 (Tue 3:30), Alan Romerero Herrera CP3
Third Presentation, presented by these students:
- In Section 173 (Tue 9:30), Lauren Hartel CP4
- In Section 174 (Tue 11:00), Tim Jaskiewicz CP4
- In Section 175 (Tue 2:00), Colin Sorge CP3
- In Section 176 (Tue 3:30), Emily Wilkerson CP3
Groups: Complete the three group works that were started by your classmates
Wed Nov 2 Meeting Discussed Section 4.4 Differentials
Fri Nov 4 Meeting Discussed Section 4.3 Optimization
Week 12 (Mon Nov 7 through Fri Nov 11)
Book Sections and (Homework Exercises)
- Section 5.1 Antiderivatives and Indefinite Integration (9-27odd, 28, 29, 31-39odd)
- Section 5.2 The Definite Integral (5-17odd, 19-22)
Exam X3 on Mon Nov 7
The Exam will be six problems, covering some of the sections from Chapters 3 & 4
- A problem about Increasing & Decreasing Functions and Relative Extrema (Section 3.3 Concepts)
- A problem about Concavity and the Second Derivative (Section 3.4 Concepts)
- A problem about Curve Sketching, making use of results from problems 1,2 (Section 3.5 Concepts)
- A problem about Related Rates (Section 4.2 Concepts)
- A problem about Optimization (Section 4.3 Concepts)
- A problem about Differentials (Section 4.4 Concepts)
Tue Nov 8 Meeting
Topic for Today: Antiderivatives
(Concepts from Section 5.1)
Book Sections and (Homework Exercises)
- Section 5.1 Antiderivatives and Indefinite Integration (9-27odd, 28, 29, 31-39odd)
In book Section 5.1, in Definition 5.1.1 at the beginning of the section, the authors present the definitions of Antiderivatives and Indefinite Integral together. I think it is useful to spend some time learning about antiderivatives before learning about indefinite integrals. In today’s meeting, you’ll learn about, and discuss, antiderivatives.
Definition of Antiderivative
- Words: \(F\) is an antiderivative of \(f\). (Note the uppercase and lower case letters!)
- Meaning: \(f\) is the derivative of \(F\). That is, \(f=F’\).
- Arrow diagram: \(F \xrightarrow[\text{take derivative}] {}f\)
In coming days, you will be learning some techniques for finding antiderivatives. We’ll start discussing those techniques on Wed Nov 9. But in today’s meeting, you will focus on the following kind of problem:
- Question: Is one given function \(f(x)\) and antiderivative of another given function \(g(x)\).
- Solution Strategy: Find \(f’(x)\) and see if it equals \(g(x)\).
[Example 1] Question: $$\text{Is }F(x)=\frac{x^3}{3}\text{ an antiderivative of }f(x)=x^2?$$ Explain why or why not. (Show the steps!)
Solution: Strategy: Find \(F’(x)\) and see if it equals \(f(x)\).
First, rewrite $$F(x)=\frac{x^3}{3}=\left(\frac{1}{3}\right)x^3$$
Now, find the derivative. $$F’(x)=\frac{d}{dx}\left(\frac{1}{3}\right)x^3=\left(\frac{1}{3}\right)\frac{d}{dx}x^3=\left(\frac{1}{3}\right)\left(3x^{3-1}\right)=x^2=f(x)$$
The answer is yes, \(F(x)=\frac{x^3}{3}\) an antiderivative of \(f(x)=x^2\), because \(F’(x)=f(x)\)
End of [Example 1]
First Presentation, presented by these students:
- In Section 173 (Tue 9:30), Ben Oldiges CP4
- In Section 174 (Tue 11:00), Bilal Tahir CP4
- In Section 175 (Tue 2:00), Olivia Keener CP4
- In Section 176 (Tue 3:30), Carlotta Datillo CP4
(Hint: Find \(F’(x)\) and see if it equals \(f(x)\).) (Show the steps clearly!)
Second Presentation, presented by these students:
- In Section 173 (Tue 9:30), Sarah Weller CP4
- In Section 174 (Tue 11:00), Andrew Champagne CP5
- In Section 175 (Tue 2:00), Jonah Lewis CP4
- In Section 176 (Tue 3:30), Kelly Koenig CP4
(Hint: Find \(F’(x)\) and see if it equals \(f(x)\).) (Show the steps clearly!)
Third Presentation, presented by these students:
- In Section 173 (Tue 9:30), Nana Asare CP5
- In Section 174 (Tue 11:00), Drew Conway CP5
- In Section 175 (Tue 2:00), Colin Sorge CP4
- In Section 176 (Tue 3:30), Alan Romero Herrera CP4
(Hint: Find \(F’(x)\) and see if it equals \(f(x)\).) (Show the steps clearly!)
Fourth Presentation, presented by these students:
- In Section 173 (Tue 9:30), Tyler Boldon CP5
- In Section 174 (Tue 11:00), Carly Doros CP5
- In Section 175 (Tue 2:00), Evan Green CP5
- In Section 176 (Tue 3:30), Reggie Shaffer CP4
(Hint: Find \(F’(x)\) and see if it equals \(f(x)\).) (Show the steps clearly!)
Groups: Work on Group Work GW25: Antiderivatives.
Week 13 (Mon Nov 14 through Fri Nov 18)
Mon Nov 14 Meeting
First Topic for Today: Indefinite Integrals (Concepts from Section 5.1)
Exercises: Section 5.1# 9-27odd, 28, 29, 31-39odd
Mark will do some Examples
Second Topic for Today: The Definite Integral (Concepts from Section 5.2)
Exercises: Section 5.2# 5-17odd, 19-22
Mark Discussed the informal definition of the Definite Integral presented in the book:
Informal Definition of the Definite Integral
- Symbol: $$\int_{x=a}^{x=b}f(x)dx$$
- Spoken: The definite integral of \(f(x)\) from \(x=a\) to \(x=b\).
- Usage: The function \(f(x)\) is continuous on the interval \([a,b]\).
- Informal Definition: the signed area of the region between the graph of \(f(x)\) and the \(x\) axis, from \(x=a\) to \(x=b\).
- Remark: This is an informal definition because we have only have a notion of area for certain basic geometric shapes. For now, this definition of definite integral can only be used in situations where the region between the graph of \(f(x)\) and the \(x\) axis, from \(x=a\) to \(x=b\), is made up of basic geometric shapes. In those situations, the value of the definite integral can be found by using familiar geometric formulas to compute the areas of the shapes that make up the region. (Note, however, that the book does not call this an informal definition. Rather, the book just presents this as the definition of the Definite Integral. That is a significant mistake in the book.)
Mark will do some Examples of Definite Integrals Gound Using Geometry
Tue Nov 15 Meeting
Students worked on Group Works involving concepts from these two sections:
- Section 5.1 Indefinite Integrals (Exercises: 5.1# 9-27odd, 28, 29, 31-39odd)
- Section 5.2 Definite Integrals (Exercises: 5.2# 5-17odd, 19-22)
The Group Works:
- GW26: Good and Bad Indefinite Integral Solutions (Section 5.1 Concepts)
- GW27: Definite Integrals for a Graph Made up of Geometric Shapes (Section 5.2 Concepts)
- GW28: Computing Definite Integrals By Using Geometry (Section 5.2Concepts)
Wed Nov 16 Meeting
Approximating Areas Using Riemann Sums
Sections for Today
- Section 5.3: Riemann Sums (Exercises: 17-39odd)
Mark Discussed the informal definition of the Definite Integral presented in the book:
Informal Definition of the Definite Integral
- Symbol: $$\int_{x=a}^{x=b}f(x)dx$$
- Spoken: The definite integral of \(f(x)\) from \(x=a\) to \(x=b\).
- Usage: The function \(f(x)\) is continuous on the interval \([a,b]\).
- Informal Definition: the signed area of the region between the graph of \(f(x)\) and the \(x\) axis, from \(x=a\) to \(x=b\).
- Remark: This is an informal definition because we have only have a notion of area for certain basic geometric shapes. For now, this definition of definite integral can only be used in situations where the region between the graph of \(f(x)\) and the \(x\) axis, from \(x=a\) to \(x=b\), is made up of basic geometric shapes. In those situations, the value of the definite integral can be found by using familiar geometric formulas to compute the areas of the shapes that make up the region. (Note, however, that the book does not call this an informal definition. Rather, the book just presents this as the definition of the Definite Integral. That is a significant mistake in the book.)
Natural Question: What do we do when the region between the graph of \(f(x)\) and the \(x\) axis, from \(x=a\) to \(x=b\), is not made up of basic geometric shapes?
That is the essence of The Area Problem.
The Area Problem
When the region between the graph of \(f(x)\) and the \(x\) axis, from \(x=a\) to \(x=b\), is not made up of basic geometric shapes,
- What does the area of the region even mean?
- How do we compute a value for the area of the region?
We start by thinking about a short wish list for Area, things that we expect to be true for Area. We don’t yet have a definition of what Area
Area Axioms
- The area of a region should be \(\geq 0\), and should \(=0\) only when the region does not contain any discs. (That’s a cheesy, but actually mathematically fine, way of waying that the region does not enclose any space.)
- The area of a region should equal the sum of the areas of the sub-regions that make up the larger region.
- (This is a consequence of axiom 2) If one region is entirely contained in some larger region, then the area of the smaller, inner region should be less than the area of the larger region.
With that third axiom in mind, we can think of a way of getting an underestimate and an overestimate for the unknown area of some curvy region by constructing a sort of sandwich involving the curvy region and two simple geometric regions. A region made up of rectangles is built in a way that it is entirely contained in the curvy region. A second region made up rectangles is built in a way that the curvy region is entirely contained in the second region.
This led to the introduction of the Left Riemann Sum with \(n\) subintervals, denoted by \(L_n\), and the Right Riemann Sum with \(n\) subintervals, denoted by \(R_n\). These sums are the area of regions made up of left rectangles and right rectangles.
Students worked on this Group Work involving calculating Left and Right Riemann Sums for a function given by a graph.
Then Mark B worked on an analogous problem involving a function given by a formula not a graph. That problem was framed as a Quest.
Quest
For the function \(f(x)\) given by the formula $$f(x)=5+\frac{x^2}{10}$$ the region between the graph of \(f(x)\) and the \(x\) axis from \(x=2\) to \(x=12\) is a curvy region, not made up of simple geometric shapes. We would like to find the area of that region.
First Work on the Quest
We don’t have a method for calculating the area of that region. We don’t even have a definition of what area even means for a region like that. But it is possible to find an underestimate and an overestimate using Riemann Sums. Mark did this with a Left Sum with \(5\) subintervals and a Right Sum with \(5\) subintervals. The result was $$L_5=94 \lt \text{ unknown area } \lt R_5=122$$
Fri Nov 18 Meeting
Sections for Today
- Section 5.3: Riemann Sums (Exercises: 17-39odd)
- Useful video Approximating areas with Sums
Meeting Part 1: Group Work: Computing Riemann Sums
Using Reference R06: Steps for Computing Riemann Sums as a guide, students worked on Group Work GW30: Computing Riemann Sums.
Meeting Part 2: The Definite Integral as a Limit of Riemann Sums
Recall our Quest from Wednesday’s meeting:
Quest
For the function \(f(x)\) given by the formula $$f(x)=5+\frac{x^2}{10}$$ the region between the graph of \(f(x)\) and the \(x\) axis from \(x=2\) to \(x=12\) is a curvy region, not made up of simple geometric shapes. We would like to find the area of that region.
We don’t have a method for calculating the area of that region. We don’t even have a definition of what area even means for a region like that. But it is possible to find an underestimate and an overestimate using Riemann Sums. Mark did this with a Left Sum with \(5\) subintervals and a Right Sum with \(5\) subintervals. The result was $$L_5=94 \lt \text{ unknown area } \lt R_5=122$$
In this part of the meeting, we will try to improve the underestimate and overestimate by using more subintervals. We use a computer tool to do the repetitive work.
Here is a handy Riemann Sum Calculator.
Rather than lecturing, Mark B will be summarizing the video Approximating areas with Sums
Students can benefit from watching the video before class.Meeting Part 3: Quiz Q08
The Quiz will be over Indefinite Integrals (concepts from Section 5.1).
Quiz Q08 on Friday Nov 18, over Indefinite Integrals (concepts from Section 5.1)
Week 14 (Mon Nov 21 through Fri Nov 25)
Book Sections and (Homework Exercises)
- Section 5.4 The Fundamental Theorem of Calculus (5-29odd, 35-57odd)
- Video that may be helpful: (video) (notes)
Mon Nov 21 Meeting
Book Sections and (Homework Exercises)
- Section 5.4 The Fundamental Theorem of Calculus (5-29odd, 35-57odd)
- Video that may be helpful: (video) (notes)
Meeting Part 1: Intro to the Fundamental Theorem of Calculus
$$\int_{x=a}^{x=b}f(x)dx\underset{\text{FTC}}{=}\left. \left(\int f(x)dx\right)\right\vert_{x=a}^{x=b}$$Meeting Part 2: Examples using the Fundamental Theorem of Calculus
Tue Nov 22 Meeting
Book Sections and (Homework Exercises)
- Section 5.4 The Fundamental Theorem of Calculus (5-29odd, 35-57odd)
- Video that may be helpful: (video) (notes)
Tue Nov 22:
- Student presentations involve showing how to find a definite integral using the Fundamental Theorem of Calculus.
- All students will have presentations
- Extra Credit Presentations (for 10 points):
- If a student is absent, another student can do their presentation for extra credit.
- Also, notice that there are 10 presentations. But no section has that many students. If there is a presentation with no student assigned to it, a student do that presentation for extra credit.
- Each student can do at most one extra credit presentation.
- The substitute student must have prepared the presentation.
- Therefore, students hoping to earn extra credit points by doing an extra presentation should prepare by studying all of the presentations and knowing how to do them.
The Fundamental Theorem of Calculus: $$\int_{x=a}^{x=b}f(x)dx\underset{\text{FTC}}{=}\left. \left(\int f(x)dx\right)\right\vert_{x=a}^{x=b}$$ Mark B introduced this theorem in lecture on Mon Nov 21. He also discusses it at length in this video and its accompanying notes. And of course the Theorem is discussed in the online Apex Calculus book, in Section 5.4.
The Presentations: (Student Numbers are shown below.)
- Show why $$\int_0^6(x+7)^2dx=618$$ That is, clearly show the steps that lead to this result.
- Show why $$\int_0^\frac{\pi}{2}\cos{(x)}dx=1$$ That is, clearly show the steps that lead to this result.
- Show why $$\int_{1}^2e^{(x)}dx=e^2-e$$ That is, clearly show the steps that lead to this result.
- Show why $$\int_{1}^{2}3^{(x)}dx=\frac{6}{\ln{(3)}}$$ That is, clearly show the steps that lead to this result.
- Show why $$\int_{16}^{49}\sqrt{x}dx=186$$ That is, clearly show the steps that lead to this result.
- Show why $$\int_{16}^{49}\frac{1}{\sqrt{x}}dx=6$$ That is, clearly show the steps that lead to this result.
- Show why $$\int_0^{\pi}(3\cos{(x)}-2\sin{(x)})dx=-4$$ That is, clearly show the steps that lead to this result.
- Show why $$\int_{75}^{100}dx=25$$ That is, clearly show the steps that lead to this result.
- Show why $$\int_1^{e^2}\frac{1}{x}dx=2$$ That is, clearly show the steps that lead to this result.
- Show why $$\int_1^{2}\frac{1}{x}dx=\ln{(2)}$$ That is, clearly show the steps that lead to this result.
Student Numbers for Section 173 (Tue 9:30)
- Nana Asare
- Tyler Boldon
- Ellie Bower
- Amy Evers
- Dalana Goddard
- Lauren Hartel
- Sara Weller
Student Numbers for Section 174 (Tue 11:00)
- Andrew Champagne
- Drew Conway
- Carly Doros
- Nicole Grant
- Tim Jaskiewicz
- Bilal Tahir
- Gavin Wolfe
Student Numbers for Section 175 (Tue 2:00
- Evan Green
- Kierston Harper
- Olivia Keener
- Austin Kiggins
- Jonah Lewis
- Dylan Pohovey
- Colin Sorge
Student Numbers for Section 176 (Tue 3:30)
- Carlotta Dattilo
- Paul Gbadebo
- Kelly Koenig
- Alan Romero Herrera
- Reggie Shaffer
- Paul Thorp
- Emily Wilkerson
Week 15 (Mon Nov 28 through Fri Dec 2)
Book Sections and (Homework Exercises)
- Section 5.4 The Fundamental Theorem of Calculus (5-29odd, 35-57odd)
- Section 6.1 Substitution (3-85odd)
Monday Nov 28 Class meeting
- Discuss The Average Value of a Function on an Interval (Concept from APEX Section 5.4)
- Discuss Position, Velocity, and Acceleration (Concepts from APEX Sections 2.2 and 5.4)
Tuesday Nov 29 Recitation
- Group Work GW31: The Average Value of a Function on an Interval
- Group Work GW32: Position, Velocity, and Acceleration
Wed Nov 30 Class meeting
- Discuss the Area So Far Function (Concept from APEX Section 5.4)
- Discuss Integration by Substitution (Concept from APEX Section 6.1)
- Refer to Reference R07: The Method of Integration by Substitution
- Quiz Q09 on Section 5.4
Fri Dec 2 Class meeting
- Discuss Integration by Substitution (Concept from APEX Section 6.1)
- Refer to Reference R07: The Method of Integration by Substitution
- Group Work GW33: Integration by Substitution
Week 15 (Mon Dec 5 - Fri Dec 9)
Final Exam, Mon Dec 5, 2:30pm - 4:30pm