
Title: Calculus for Business, Economics, Life Sciences, and Social Sciences, Brief Version, 14th Edition
Authors: Barnett, Ziegler, Byleen, Stocker
Publisher: Pearson, 2019
ISBN 13: 978-0-13-486264-4
Remark: The ISBN number listed above is for
Sections, Content, Homework, and Videos:
Point out that the Blackboard Site will only be used for a few things:
Urge the students to go to be Blackboard site right away and follow the instructions for getting MyLab configured, so that they can begin work on their homework.
Show them how they can always find their way to the MATH 1350 Web Page by going first to the Blackboard site and finding the link there.
Or they can bookmark the MATH 1350 Web Page in their web browser and navigate to it directly: Link to MATH 1350 Web Page
Discuss the Two Components of the Course Format
Discuss the Grading.
Discuss the Attendance Policy.
Discuss the Calendar.
Discuss the Required Computer Tools.
Discuss the Study Routine for the Student.
Instructor: In Section 2.1 of the textbook, and in Limits Videos A, B, C, D, E, you will learn about limits. It is important to understand the distinction between the following two symbols:
This is made more precise in the official Definition of Limit:
The Definition of Limit
One kind of problem that shows up in the examples in that video and in your Homework H02 is the following type:
Instructor Example #1: (See the [Example 1] in the Notes for Limits Video A.) For the function shown in the graph shown below, find the following two things and explain how they are found.
$$f(6) = \ ?$$ $$\lim_{x\rightarrow6}f(x) = \ ?$$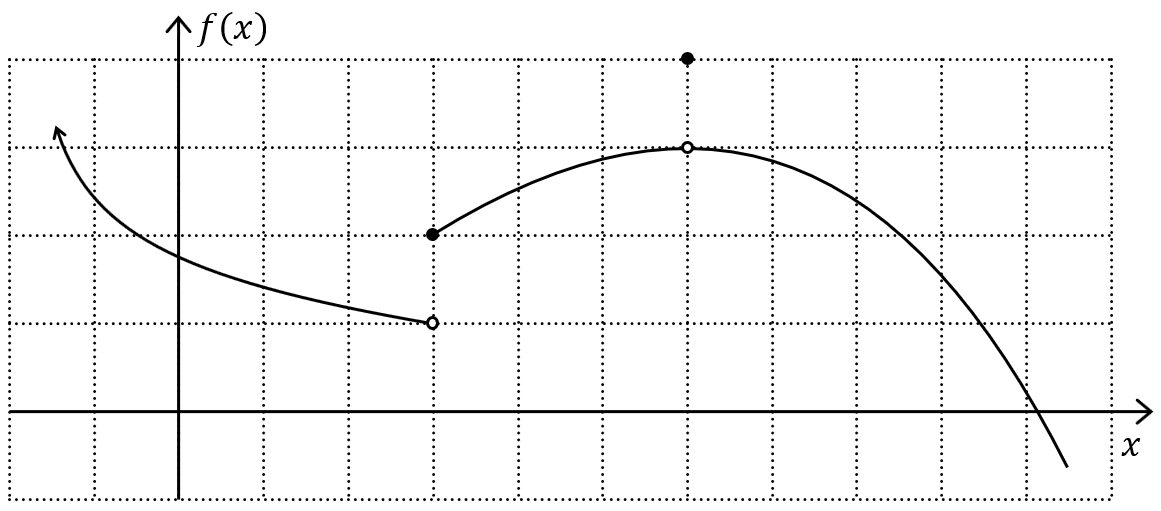
Instructor Example #2: For the same function shown in the graph above, find the following two things and explain how they are found.
$$f(3) = \ ?$$ $$\lim_{x\rightarrow3}f(x) = \ ?$$Instructor: Introduce the concept of limit from the left and limit from the right.
$$\lim_{x\rightarrow3^-}f(x)$$ $$\lim_{x\rightarrow3^+}f(x)$$Instructor Example #3: For the same function shown in the graph above, find the following two things and explain how they are found.
$$\lim_{x\rightarrow3^-}f(x)= \ ?$$ $$\lim_{x\rightarrow3^+}f(x)= \ ?$$Instructor: Discuss Class Drill: Limits for a Function Given by a Graph .
Instructor: In Section 2.1 of the textbook, and in Limits Videos A, B, C, D, E, you learn about limits. In the previous class meeting, we discussed the distinction between the following two symbols:
This is made more precise in the official Definition of Limit:
The Definition of Limit
Two kind of problems that show up in the examples in the Videos and in your Homework for Section 2.1 are the following types:
From the Homework for Section 2.1, you know that, in general, the value of \( \lim_{x\rightarrow c}f(x) \) might not be the same as the value of \( f(c)\).
In Limits Video B [Example 1] , on page 4 of the notes, the discussion turns to problems of the following type:
The first example involves the function \(f(x)=-7x^2+13x-25\). First, the \(y\) value \(f(-2)\) is computed, and found to be
$$f(-2)=-79$$The second part of the example is about estimating the value of the limit
$$\lim_{x\rightarrow -2} f(x)$$To estimate the limit, tables of \(x,y\) values are made, with the \(x\) values getting closer and closer to \(-2\), but not equal to \(-2\). It looks as though the values of \(f(x)\) are getting closer and closer to \(-79\). Based on this observation, we estimate the limit:
$$\lim_{x\rightarrow -2} f(x) \underset{estimate}{=} -79$$Immediately following the example are two Remarks.
Remark #1 is a comparison of the limit and the \(y\) value. An important point is made:
Even though, in this first example of a function \(f(x)\) given by a formula, it happens that the value of the limit does match the \(y\) value, that does not always happen.
Remark #2 is about the unsatisfying nature of the method of estimating the value of a limit by making a table of \(x,y\) values. An important question is raised:
Question: Is there is a better way? That is, is there some way to analyze the formula for \(f(x)\) to determine the value of the limit precisely, without estimating?
Answer: There are analytical techniques, developed in higher-level math, that provide a way of analyzing the formulas for certain kinds of functions to determine their limits.
The analytical techniques, themselves, are beyond the level of an introductory Calculus course. But the general results of using the techniques can be presented as Theorems that can be used in our course. Three such Theorems about Limits are presented on pages 10,11 of Limits Video B. These Theorems are the tools used in an Analytical Approach to Finding Limits.
Instructor: In the Homework for Section 2.1, you solve problems involving finding limits where the function \(f(x)\) is given by a formula:
we'll start with a couple examples of similar problems.
Instructor do [Example 1] on Chalkboard (This example is similar to Limits Video B [Example 2].) For the function
$$f(x)=\sqrt{65+x^2}$$Find the following using the Theorems about Limits presented earlier.
Instructor do [Example 2] on Chalkboard (This example is similar to Limits Video B [Example 3].) For the function
$$f(x)=\frac{x^2-8x+12}{x^2-13x+42}=\frac{(x-2)(x-6)}{(x-7)(x-6)}$$Find the following using the Theorems about Limits presented earlier.
Instructor: In the Homework for Section 2.1, you begin studying more advanced limits where the function \(f(x)\) is given by a formula and where the value of \( \lim_{x\rightarrow c}f(x) \) is not always the same as the value of \( f(c)\). Some of the functions that exhibit this behavior are rational functions. That is, they are ratios of polynomials.
Before embarking on learning about the new, more advanced kind of limit, it is important to review three concepts involving ratios:.
Instructor: A third type of limit of a quotient, one that we have not yet considered, is the case when the limit of the numerator and the limit of the denominator are both zero. That is, $$\lim_{x\rightarrow c} \frac{numerator}{denominator}$$ where
The next example involves a limit that is an indeterminate form. The example is based on problems that you work on in the Homework for Section 2.1, problems involving rational functions. A description of the problem type is
These H06 problems involve the most important concept of the first month of Calculus
This is central to the question
Instructor: Do [Example 3] (This example is similar to Limits Video D [Example 1].) For the rational function \(f(x)\) defined below
$$ f(x) = \frac{x^2+x-6}{x-2} =\frac{(x-2)(x+3)}{(x-2)} $$Show how to find the following:
Remark: As a general rule, if a limit \(\lim_{x\rightarrow c}f(x)\) is not an indeterminate form, then the value of the limit will be the same as the value of the \(y\) value, \(f(c)\). (That is, either both will have the same numerical value, or both will not exist.) On the other hand, if a limit \(\lim_{x\rightarrow c}f(x)\) is an indeterminate form then the limit may or may not exist. But the \(y\) value \(f(c)\) will definitely not exist. So limits of indeterminate forms are examples where the value of the limit of a function can differ from the \(y\) value of the function.
A shortcoming of our textbook and the MyLab system is that none of the exercises about limits ask you to both compute a \(y\) value and compute a limit, so you might not realize that those results can differ, and so you might not realize the significance of the limit. In the videos, discussion of limits of indeterminate forms is in Limits Video D. In that video, the examples do involve both computing \(y\) values and computing limits. Be sure to watch that video and study the accompanying notes, so that you understand the significance of the limits.
Instructor: On Wednesday, we discussed limits, and ended the meeting with a discussion of limits of particular kinds of quotients. These limits were indeterminate forms. That is, they were limits of quotients with the property that the limit of the numerator and the limit of the denominator are both zero. That is, $$\lim_{x\rightarrow c} \frac{numerator}{denominator}$$ where
Limits of difference quotients are difficult because of the number of steps involved.
Correctly computing this limit will, at some point, involve knowing to cancel \(\frac{h}{h}\). This is another occurence of the most important concept of the first month of Calculus
Students will encounter such limits in the homework for Section 2.1. They are discussed in Textbook Section 2.1 and in Limits Video E. In our first Class Drill of the semester, you will do an example of this type.
For the function $$f(x) = x^2+5x+7$$ the goal is to find the value of the difference quotient
$$\lim_{h\rightarrow 0}\frac{f(3+h)-f(3)}{h}$$Do this in two steps.
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see [Example 1] on page 6 of the Notes for Limits Video E.)
Instructor: So far, when we have discussed limits, the symbol $$\lim_{x \rightarrow a}f(x)=b$$ means that the graph of \(f(x)\) appears to be heading for the location \( (x,y)=(a,b) \). The symbol gives information about a trend in the graph.
This is made more precise in the official Definition of Limit in Limits Video A, on page 4 of the notes.
Realize that in that definition of limit, the letters \(a\) and \(b\) represent real numbers. That definition of limit could actually be thought of as describing two trends:
The definition of limit presented above is from Textbook Section 2.1 (content discussed in Limit Videos A,B,C,D,E).
Starting in Textbook Section 2.2 (content discussed in Video H10), the definition of limit is changed. The definition is expanded, so that the definition encompasses more types of trends in the behavior of the \(x\) and \(y\) values. The kinds of trends that will be included in the new, expanded definition of limit are
New terminology, and new symbols, will be used to abbreviate particular pairs of trends: a trend in the \(x\) values and the corresponding trend in the \(y\) values.
Here's the first new term that is part of the expanded definition of limit: Infinite Limit.
Instructor: Project The Definition of Infinite Limits, from Video10. Discuss the graphical significance, involving vertical asymptotes. And discuss the significance of the phrase without bound.
Notice that this definition describes the following pair of trends:
There are many variations of the basic definition of Infinite Limit. Some variations are presented in the textbook, and in the videos and their notes. But not all possible variations are presented. That would be too tedious to read. The idea is that you need to be able to figure out how to read, write, speak, and illustrate the variations.
Instructor: Do the following [Example 1] about the Basic Notation of Infinite Limits (See the Notes from the Video for H10.)
Instructor: Do the following [Example 2] about Infinite Limits (See the Notes from the Video for H10).
Suppose that you are told that the graph of some function \(g(x)\) has the following behavior
Here's another new term that is part of the expanded definition of limit: Limit at Infinity.
Instructor: Project The Definition of Limits at Infinity, from Video10. Discuss the graphical significance, involving horizontal asymptotes.
Notice that this definition describes the following pair of trends:
As was the case with the definition of Infinite Limit, there are also variations of the basic definition of Limit at Infinity. You’ll explore these in a Class Drill.
Suppose that you are told that the graph of some function \(g(x)\) has the following behavior
Instructor: Show the solution to the Class Drill that the class just worked on. (For Reference, see the Notes from the Video for H10.)
Sections, Content, Homework, and Videos:
Instructor: On Friday, we discussed an Expanded Definition of Limit, that involved the terminology and notation of infinity. The first kind of limit that we discussed as part of the expanded definition of limit was the Infinite Limit.
Instructor: Project The Definition of Infinite Limits.
Remember that this definition describes the following pair of trends:
In Friday's meeting, we considered examples where function is given by a graph. That is, examples of the following form:
Finding an infinite limit is fairly easy when the function is given by a graph. But computing an infinite limit is difficult when the function is given by a formula. That is, problems of this type:
Some computations of this type are discussed in the Video for H11.
For the function
$$ f(x) = \frac{3}{x-2} $$We are interested now in finding the following limit: $$ \lim_{x \rightarrow 2^+} f(x) $$ But as discussed in the Video for H11, the computation of this limit is done in different ways, depending on whether one is using the word limit in the sense of Section 2.1 (the original definition of limit, in which the concept of infinity is not used) or in the sense of Section 2.2 (the expanded definition of limit, in which the concept of infinity is used)
Let \(f(x)\) be the function
$$ f(x) = \frac{-5}{x+3} $$Using the techniques of Section 2.1 (the original definition of limit, in which the concept of infinity is not used, the value of the limit is
$$ \lim_{x \rightarrow -3^+} f(x) \ DNE $$Explain how that result is obtained. (Show the calculation clearly, with explanations.)
Instructor: Show the solution to the Class Drill that the class just worked on. (See the Notes from the Video for H11. In particular, study pages 1 - 4.)
Instructor: Show the solution to the Class Drill that the class just worked on. (See the Notes from the Video for H11. In particular, study pages 1 - 8.)
Instructor: It is important to know how to use the correct solution methods for these limits involving infinity. It is common for students to have learned some kind of shortcut method for reaching an answer. Realize that these shortcut methods often give the wrong answer. For example, consider the Invalid Solutions presented in the Notes from the Video for H11 on pages 11 & 12. Even if an invalid solution method happens to give the correct answer in some particular instance, the method is still invalid.
More importantly, a shortcut method for reaching an answer (whether that answer is right or wrong) does not convey any understanding of why the answer comes out the way it does. You won't really understand what you are doing, and you won't be able to explain what you did to anybody else.
It is also important to note that when computing limits of the sort computed in your Class Drills, it is important to know whether to use the original definition of limit (in which the concept of infinity is not used), or the expanded definition of limit (in which the concept of infinity is used). In the Textbook and MyLab, it can sometimes be ambiguous. In general, in the Textbook and MyLab,
Questions for the instructor to pose to students.
Instructor: Here are two important observations about the questions that you just answered.
Observation 1: In formulating your answers about the limits of the polynomial functions you (hopefully) made up some new notation to abbreviate a new kind of limit involving infinity that we have not seen before. That is, the symbol $$ \lim_{x \rightarrow \infty} f(x) = -\infty$$ describes the following pair of trends in the right end of the graph of \(f(x)\):
(Of course, you also made up other new notation to describe variations on this idea.)
Observation 2: Realize that questions about end behavior, horizontal asymptotes, and limits at infinity are all related. They all involve $$\lim_{x\rightarrow \infty}f(x) \ \ \text{or} \ \ \lim_{x\rightarrow -\infty}f(x)$$
Instructor: On Monday, we began discussing the idea of the end behavior of a function. The right end behavior is a description of whether the right end of the graph goes up (or down) without bound, or levels off, or does something else. If the right end of the graph levels off, approaching a height \(y=b\), we say that the graph has a horizontal asymptote on the right, with line equation \(y=b\).
On Monday, we discussed that questions about end behavior, horizontal asymptotes, and limits at infinity are all related. They all involve $$\lim_{x\rightarrow \infty}f(x) \ \ \text{or} \ \ \lim_{x\rightarrow -\infty}f(x)$$
On Monday, we only considered the end behavior (and limits at infity) of polynomial functions. Today, we'll discuss the end behavior of rational functions. (Remember that these are functions that are ratios of polynomials.)
Question for the instructor to pose to students:
Consider rational function $$ f(x) = \frac{2x^2-6x-8}{3x^2-3x-36} $$
Instructor: Discuss the following:
Note to Students: In MATH 1350, on Quizzes and Exams, you will need to be precise in your descriptions of asymptotes. For instance, for the example just considered, it would not be sufficient to say that
Your description of asymptotic behavior needs to indicate whether the asymptote is horizontal or vertical. Furthermore,
Class Drill: Finding limits at infinity.
Instructor: Have students work on this Class Drill.
Instructor: Show the solution to the Class Drill that the class just worked on. (See the Notes from the Video for H13.)
Instructor: We have seen that the limit behavior \(\lim_{x\rightarrow c}f(x) = \infty \) corresponds to the graph behavior that \(f(x)\) has a vertical asymptote with line equation \(x=c\), and that the graph goes up along both sides of that asymptote.
And we have seen that the limit behavior \(\lim_{x\rightarrow \infty}f(x) = b \) corresponds to the graph behavior that \(f(x)\) has a horizontal asymptote on the right with line equation \(y=b\)
The computation of the limit can be time consuming when you are first starting out. But after you do enough of those kinds of limits, you begin to see some patterns emerge. Once you begin to notice those patterns, you may be able to give the values of some limits, or find the line equations for some asymptotes, by simply scrutinizing the formula for a function, rather than by going through all of the steps to find a limit.
That is the idea behind questions that ask you to "find all the horizontal & vertical asymptotes" for a rational function.
This concept is discussed indirectly in various places in the textbook Section 2.2. In the videos, the Video for H15 is specifically about the concept. Most importantly, key results are presented on pages 5 and 7 of the Notes from the Video for H13. (Instructor, project and discuss those pages.)
Question for the instructor to pose to students:
Find all horizontal and vertical asymptotes for the rational function
$$ f(x) = \frac{7x^2-28x-35}{3x^2-27x+60}$$(Be sure to give line equations for the asymptotes. That is, give equations of the form \(x=a\) or \(y=b\). And be sure to say whether each asymptote is horizontal or vertical.)
Quiz Q1 during the last 20 minutes of the Wed May 22 class meeting
No Books, no Notes, no Calculators, no Phones, no Smart Watches
The quiz material is taken from the material covered in Section 2.1 and Section 2.2. See the List of Homework Assignments for links to the corresponding Instructional Videos.
A Suggestion for Studying: When you work on your homework in MyLab, write down your complete solutions to each problem on paper before you type the answer into MyLab. Focus on the clarity and correctness of your written solution. Keep your written work organized in a notebook. Compare your written work to the written examples in the Videos. If possible, find another student, or a tutor, or your instructor, to look over your written work with you. Even though MyLab does not require that you write stuff down, you will learn a lot by focusing on your written work.
Fri May 24 is the last day to drop without a "W" and the last day to drop without being charged for access to the MyLab Digital Course Materials.
Instructor: Given a graph for a function \( f(x) \), it is easy to spot funky features like holes, jumps, and points in the wrong place on the graph. If a function \( f(x) \) is given by a formula, rather than a graph, it would be nice to have some way of analyzing the formula for \( f(x)\) to determine where its graph might have those funky features. The Definition of Continuity presents a test that can be performed on the formula for a function \( f(x)\).
Definition of Continuity at a particular \(x\) value
Definition of Continuity on an interval
Instructor: Have students work on the following Class Drill:
Instructor: Present a solution to the Class Drill that the class just worked on.(See the Notes from the Video for H16.)
Instructor: Given a graph for a function \( f(x) \), it is easy to spot portions of the graph that are above or below the \(x\) axis. (Show Page 2 of the Notes from the Video for H20.)
If a function \( f(x) \) is given by a formula, rather than a graph, then it would be nice to have some way of analyzing the formula for \( f(x)\) to determine where its graph is above or below the \(x\) axis. In other words, where the \( y \) values are positive, negative, or zero.
Two important observations are the following:
Based on those two observations, we realize that to determine the sign behavior of a function given by a formula, it is helpful to first determine the \(x\) values where the function has an \(x\) intercept or is discontinuous. We give these \(x\) values a name:
Definition: A partition number for a function \(f\) is an \(x\) value where \(f\) is discontinuous or \(f(x)=0\).
On the intervals between the partition numbers for \(f\), the sign of the function \(f\) does not change.
This allows us to articulate a procedure for determining the sign behavior of a function using what we call a sign chart.
PROCEDURE: Constructing Sign Charts
Given a function \(f\)
Step 1: Find all partition numbers of \(f\):
Step 2: Plot the numbers found in Step 1 on a real number line and indicate the sign behavior of \(f\) at each partition number. (Is \(f(x)=0\) or does \(f(x)\) not exist) Observe that this will divide the number line into intervals.
Step 3: Select a test number in each open interval determined in step 2 and evaluate \(f(x)\) at each test number to determine whether \(f(x)\) is positive (+) or negative (-) in each interval. Show each sign calculation clearly, and put the result (+) or (-) above the number line in the corresponding interval.
Step 4: Title your diagram: "Sign Chart for \(f(x)= formula\)."
Instructor: Have students work on the following Class Drill:
Instructor: Show the solution to the Class Drill that the class just worked on. (See the Notes from the Video for H21. In particular study pages 1 - 7.)
Observe the difference between the sign chart made in Question 1 and the sign chart made in Question 2:
Furthermore, notice that if the sign calculations are done clearly, it is possible to understand why the signs are changing or not changing.
Indeed, in the example that I just did,
Sections, Content, Homework, and Videos:
Instructor: Recall that on Friday, we discussed a procedure for determining the sign behavior of a function given by a formula. That is, a procedure for determining where the function is positive, negative, or zero. And recall that a key part of the procedure was the concept of partition numbers.
Definition: A partition number for a function \(f\) is an \(x\) value where \(f\) is discontinuous or \(f(x)=0\).
Remember that on the intervals between the partition numbers for \(f\), the sign of the function \(f\) does not change.
This allows us to articulate a procedure for determining the sign behavior of a function using what we call a sign chart.
PROCEDURE: Constructing Sign Charts
Given a function \(f\)
Step 1: Find all partition numbers of \(f\):
Step 2: Plot the numbers found in Step 1 on a real number line and indicate the sign behavior of \(f\) at each partition number. (Is \(f(x)=0\) or does \(f(x)\) not exist?) Observe that this will divide the number line into intervals.
Step 3: Select a test number in each open interval determined in step 2 and evaluate \(f(x)\) at each test number to determine whether \(f(x)\) is positive (+) or negative (-) in each interval. Show each sign calculation clearly, and put the result (+) or (-) above the number line in the corresponding interval.
Step 4: Title your diagram: "Sign Chart for \(f(x)= formula\)."
On Friday, we only used sign charts to determine the sign behavior of functions. Today we will again discuss sign charts, but as part of a larger problem: solving inequalities. Here is a Class Drill involving making a sign chart for a function and then using the sign chart to solve an inequality
Instructor: Have students work on the following Class Drill.
Instructor: Present a solution to the Class Drill that the class just worked on. (See [Example 1] on page 7 of the Notes from the Video for H21.)
Instructor: Sometimes, inequalities can be more difficult to solve simply because the partition numbers are harder to determine. Finding partition numbers involves solving equations. There are skills involved, and also some common mistakes to be avoided. We'll discuss one.
Instructor: Pose this question to the students.
Frick and Frack are trying to solve the equation $$ x^3 = 25x $$ Frick does the following: He divides by \( x \) to get the new equation $$ x^2 = 25 $$ Then he says that the solution is $$ x=5 $$ Frack does the following: He divides by \( x \) to get the new equation $$ x^2 = 25 $$ Then he says that the solution is $$ x=5, x=-5 $$ Is Frick right? Is Frack right? Explain.
Instructor: Inequalities are generally tricky things to solve. Sometimes, they can be made easier to solve by finding an equivalent inequality that has the number \(0\) on one side. Then the inequality can be solved by finding when the expression on the other side is greater than \( 0 \) or less than \(0\). The sign chart is a useful way to structure the solution of the problem. In this Class Drill, you will find the solution to an inequality by first finding an equivalent inequality that has the number \(0\) on one side and then solving that inequality.
Instructor: Have students work on the following Class Drill.
Solve the inequality $$ x^3 \lt 25x $$ Present the solution set 3 ways:
Instructor: Present a solution to the Class Drill that the class just worked on. (See [Example 3] on page 10 of the Notes from the Video for H21.)
Instructor: Section 2.4 is basically about the calculations of the slopes and equations of secant lines and tangent lines. The computations can be messy, and in some cases difficult, so that students might not really understand what those computations mean. Although textbook examples often include illustrations of the calculations, the homework problems in the MyLab system rarely ask the student to visualize or illustrate the meaning of the computations. Making illustrations of a computation is usually not nearly as hard as the computation, and the making of the illustration can improve students' understanding of the computation, so it is worthwhile to take some time to make a drawing. In a Class Drill, you will work on making a drawing to illustrate a calculation that you did in Homework H25.
Instructor: Have students work on the following Class Drill.
In Homework H25 problem [1](A), you were asked to compute a quantity of the following form: $$ \frac{f(b)-f(a)}{(b)-(a)} $$ This Class Drill is based on that problem.
Let \( f(x) = 7-x^2\).
Instructor: Show the solution to the Class Drill that the class just worked on. (See [Example 1](C) on page 4 of the Notes from the Video for H25.)
Instructor: Most students are comfortable with equations like $$y=7x^2-13x+27$$ but less comfortable with function notation like $$f(x)=7x^2-13x+27$$ Calculus involves a lot of working with functions and function notation, and understanding the meaning of expressions that have something instead of just \(x\) inside the \(f(x)\). Throughout today's meeting, we'll encounter questions about building and simplifying expressions that involve something instead of just \(x\) inside the \(f(x)\).
Instructor: Pose this question to the students.
For the function $$f(x)=x^2+3$$ Frick and Frack are trying to find $$f(x+2)$$ Frick does the following: \begin{eqnarray} f(x+2) &=& x^2+3+2 \\ &=& x^2 + 5 \end{eqnarray} Frack does the following: \begin{eqnarray} f(x+2) &=& (x+2)^2+3 \\ &=& x^2+2^2+3 \\ &=& x^2+4+3 \\ &=& x^2+7 \end{eqnarray}
Question for the Class: Is Frick right? Is Frack right? Explain.
Answer: Frick and Frack are both wrong!! Here is the correct calculation:
\begin{eqnarray}f(x) &=& x^2+3 \\ f( \ \ ) &=& ( \ \ )^2+3 \ \ (empty \ version) \\ f(x+2) &=& (x+2)^2+3 \\ &=& (x+2)(x+2)+3 \\ &=& x^2 + 2x + 2x + 4 + 3 \\ &=& x^2 + 4x + 7 \end{eqnarray}Instructor: An expression of the form $$ \frac{f(2+h)-f(2)}{h} $$ is called a difference quotient. We will discuss why that name is used in a few minutes. But first, you will do a Class Drill involving building and simplifying a difference quotient
Instructor: Have students work on the following Class Drill.
For the function $$f(x)=3x^2-5x+1$$ Instructor: Find the following
Instructor: Show the solution to the Class Drill that the class just worked on. (See the Notes from the Video for H24.)
Instructor: Now we'll discuss why expressions like the expression $$ \frac{f(2+h)-f(2)}{h} $$ that I just built and simplified are called difference quotients.
Let's back up and consider how we compute the slope of a line. Suppose that \((x_1,y_1)\) and \((x_2,y_2)\) are distinct (that is, not the same) points on a non-vertical line. The slope of the line is found by computing
$$m=\frac{\Delta y}{\Delta x} =\frac{y_2 - y_1}{x_2 - x_1}$$Notice that this expression is a quotient. Also notice that the expression in the numerator is a difference of \(y\) values. And notice that the expression in the denominator is a difference of \(x\) values. So the expression is a quotient of differences. We could also say that the expression is a difference quotient.
Now consider the graph of a function \(f(x)\). The ordered pair \((2,f(2))\) represents a point on the graph of \(f(x)\), and the ordered pair \((2+h,f(2+h))\) represents a point on the graph of \(f(x)\). If \(h \neq 0\), then the expressions represent distinct (that is, not the same) points. In this case, there is exactly one line that passes through the two points. The slope of this line would be computed by the following computation
$$m=\frac{\Delta y}{\Delta x} =\frac{y_2 - y_1}{x_2 - x_1}=\frac{f(2+h)-f(2)}{(2+h) - h}=\frac{f(2+h)-f(2)}{h}$$As discussed above, we could call this expression a difference quotient.
Instructor: Most students are comfortable with the concept of quantifying the steepness of a line by finding the slope of the line. A major concept in Calculus is learning how to quantify the steepness of a curvy graph at a given point on the graph. This is done by associating a line to the graph at the given point, and finding the slope of that line. The line is called the tangent line. You have learned about tangent lines in your reading and in your homework videos, and we will be discussing them in today's meeting. But before learning about tangent lines, it is important to review the terminology and computations involved when working with slopes and equations of lines. In this Class Drill, you will find the point-slope form and slope-intercept form of the equation of a line.
Class Drill: (Material from Homework H23 involving Prerequisite Skills, so there is no video) For the line that passes through the point \( (3,7) \) and that has slope \( m=1 \), do the following.
Instructor: Show the solution to the Class Drill that students just worked on.
Instructor: In the Video for H25, you were introduced to the Instantantaneuous Rate of Change, the tangent line and a discussion of the computation of the slope of the tangent line. Here are the first two definitions:
Definition of Instantaneous Rate of Change
An important concept for the next month of the course is the relationship between the derivative, the tangent line, and rate of change:
In a Homework problem, you are asked to compute the slope of the graph of a given function of the form \( f(x)=ax^2 \) at a particular given point. This Class Drill is based on that problem.
Instructor: Show the solution to the Class Drill that the class just worked on. (See [Example 1](E),(F) on pages 9 - 12 of the Notes from the Video for H25.)
Quiz Q2 during the last 20 minutes of the Fri May 31 class meeting
No Books, no Notes, no Calculators, no Phones, no Smart Watches
The quiz material is taken from the material covered in portions of Section 2.2 and Section 2.3. See the List of Homework Assignments for links to the corresponding Instructional Videos.
Sections, Content, Homework, and Videos:
There are a lot of difficult computational skills to learn in Section 2.4. But there is also a lot of new terminology and notation. Sometimes it is helpful to just focus on some of the terminology and notation, and think about what it means without having to do a difficult calculation. Here is a Class Drill that is just about recognizing what certain symbols and terms mean.
[Drill for the Class] (See the Notes from the Video for H25.) Shown below is a list of seven phrases and mathematical expressions that each represent a number. Each of these phrases and mathematical expressions is discussed in the Video for H25.
Question for the Class: What are the members of the two groups?
One Group:
The Other Group:
Instructor: In the Video for H25, you learned that the expression $$m=\lim_{h\rightarrow0}\frac{f(a+h)-f(a)}{h}$$ computes a number \(m\) that is the slope of the line tangent to the graph of \(f(x)\) at \(x=a\). In this expression, \(a\) is a number and the result of the calculation is a number \(m\).
In the Video for H26, you learned about replacing the number \(a\) with a variable \(x\). The resulting expression $$f'(x)=\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{h}$$ would not represent a number, but rather would represent a function of \(x\). That function is called the derivative of \(f\). Here is the full definition:
Computing \(f'(x)\) using the Definition of the Derivative is difficult and messy.
Some of you may have studied calculus before and know about shortcuts to finding derivatives. The shortcuts are not nearly so difficult and not nearly so messy.
We learn the shortcuts in this course, too. They are called Derivative Rules. But they come later, starting in Section 2.5 of the book, with homework coverage starting in Homework H29. We'll begin discussing those easier methods next week. In this meeting, we will discuss two examples involving finding derivatives using the Definition of the Derivative. That is, the harder, messier method. Problems of this sort are among the most difficult problems that you will do in MATH 1350. The Examples will be done as Class Drills.
Instructor: Have students work on these two Class Drills.
Let \(f(x)=5x^2-7x+3\)
Instructor: Show the solution to the problem that the class just worked on in the Class Drill. (See [Example 1]on page 9 of the Notes from the Video for H26.)
Let \(f(x)=5+\frac{7}{x}\)
Instructor: Show the solution to the problem that the class just worked on in the Class Drill. (See [Example 1] on pages 4 - 10 of the Notes from the Video for H27.)
Instructor: Notice that the computation done in the second Class Drill involved a lot of steps, a lot more than the computation done in the first Class Drill. But notice that although the computation for the second Class Drill involved a lot of steps, there were no tricks in the computation. It was necessary to find a common denominator for two fractions, and that led to a mess of work. But finding a common denominator is not mysterious. You learned the basic idea of it in grade school.
Instructor: If there is enough time remaining in the meeting, present this Example.
In the two Class Drills that you just worked on, you used the Definition of the Derivative to find the derivative of a polynomial function and a \(1/x\) type function. A type of function that is simpler than either of these types is the linear function. That is, a function of the form $$ y=mx+b$$ Because linear functions are relatively simple, one would expect that computing their derivatives, using the Definition of the Derivative, would also be relatively simple.
Well, it is true that the computation is relatively simple. But students are often confused by that very simplicity. Terms that students are used to seeing in the computation of the derivative of most functions are just not present in the computation of the derivative of a linear function. You have a problem involving finding the derivative of a linear function in your Homework for Section 2.4. You may find it confusing. For that reason, it is worthwhile for the instructor to do an example. (If there is not time in the meeting for the instructor to do this example, students can see the very similar [Example 2] on pages 14 - 17 of the Notes from the Video for H26.)
Let \(f(x)=5+\frac{7}{x}\)
Instructor: Recall that on Monday, we discussed the Definition of the Derivative.
Also on Monday, you did two Class Drills in which used the Definition of the Derivative to compute derivatives
We'll begin today's meeting with computation of a derivative using the Definition of the Derivative. You'll see that today's computation will be as messy as the computation of the derivative of \(f(x)=5+\frac{7}{x}\) on Monday. But not only is today's computation messy, it also involves a trick. You learned about the trick in your reading and in the Video for H27, and you use the trick in your solution to at least one of the homework problems from Section 2.4. Here is a review of the Trick.
Consider the limit $$\lim_{h\rightarrow 0}\frac{\sqrt{x+h}-\sqrt{x}}{h}$$ If we try substituting \(h=0\) into the expression, we obtain $$\frac{\sqrt{x+(0)}-\sqrt{x}}{(0)}=\frac{\sqrt{x}-\sqrt{x}}{0}=\frac{0}{0}$$ This result DOES NOT tell us that the limit is undefined. Rather, it only tells us that the limit is an indeterminate form, and that we are not allowed to simply substitute \(h=0\). Instead, we must first do some work to eliminate the indeterminate form.
The work that we do is the following trick: We multiply the numerator and denominator of the fraction by the same particular expression, to obtain a new fraction. This doesn't change the meaning of the limit, because we are just multipling the fraction by \(1\). But if we simplify the new fraction, we will end up with a form that will allow us to cancel something, and thereby eliminate the indeterminacy.
Here are the details of the calculation: $$\begin{eqnarray} \lim_{h\rightarrow 0}\frac{\sqrt{x+h}-\sqrt{x}}{h} &\underset{\text{ Trick }}{=} & \lim_{h\rightarrow 0}\frac{\sqrt{x+h}-\sqrt{x}}{h} \cdot \frac{\left(\sqrt{x+h}+\sqrt{x}\right)}{\left(\sqrt{x+h}+\sqrt{x}\right)} \text{ (still indeterminate)}\\ &=& \lim_{h\rightarrow 0}\frac{\sqrt{x+h}\sqrt{x+h}-\sqrt{x}\sqrt{x+h}+\sqrt{x}\sqrt{x+h}-\sqrt{x}\sqrt{x}}{h\left(\sqrt{x+h}+\sqrt{x}\right)} \text{ (still indeterminate)}\\ &=&\lim_{h\rightarrow 0}\frac{(x+h)-(x)}{h\left(\sqrt{x+h}+\sqrt{x}\right)} \text{ (still indeterminate)}\\ &=& \lim_{h\rightarrow 0}\frac{h}{h\left(\sqrt{x+h}+\sqrt{x}\right)} \text{ (still indeterminate)} \\ & \ &\text{Because }h\rightarrow 0\text{, we know that }h \neq 0\text{, so we can cancel }\frac{h}{h} \\ &=& \lim_{h\rightarrow 0}\frac{1}{\sqrt{x+h}+\sqrt{x}} \text{ (no longer indeterminate, so we are allowed to just substitute in }h=0\text{)} \\ &=& \frac{1}{\sqrt{x+(0)}+\sqrt{x}} \\ &=& \frac{1}{\sqrt{x}+\sqrt{x}} \\ &=& \frac{1}{2\sqrt{x}} \end{eqnarray} $$
You'll do a similar computation in the following Class Drill.
Instructor: Have students work on the following Class Drill:
Let \(f(x)=5+7\sqrt{x}\)
Instructor: Show the solution to the Class Drill that the class just worked on. (See [Example 2] on pages 11 - 15 of the Notes from the Video for H27.)
Instructor: The Tangent Line is introduced on page 11 of the Notes from the Video for H25. We discussed the Tangent Line during this past Friday's class meeting. Recall the definition:
The example that the Instructor did on Friday was about finding the slope of the tangent line. This involved computing the number \(m=f'(1)\).
It is often useful to know not only the slope of the tangent line, but also the equation of the tangent line. (Since the tangent line is a line, its equation will be a line equation.) Problems involving the equation of a tangent line first appear in Section 2.4 of the book, in your Homework for Section 2.4, and then they appear throughout the rest of Chapter 2 and in Chapter 3. Let's review the form of the equation of a tangent line.
Knowing the two properties of the tangent line introduced above, we are able to write down a general form for the equation for the tangent line. It is discussed on page 13 of the Notes from the Video for H25. The general form (as discussed in the video notes) is
In this Class Drill, you'll find the equation for a tangent line.
Instructor: Have students work in groups of on the following Class Drill:
The goal is to find the equation of the line tangent to the graph of \(f(x)=x^2-4x+8\) at \(x=3\).
Instructor: Show the solution to the Class Drill that the class just worked on. (See [Example 1] on pages 11 - 15 of the Notes from the Video for H25.)
Instructor: If there is time remaining, disucuss the following Topic:
Some simple problems give you information about the values of \(a,f(a),f'(a)\) and ask you to give the equation of the tangent line. These problems are simpler in the sense that you don't have to do the computation of the parts \(f(a)\) and \(f'(a)\), because those quantities are given to you. But you still have to know the general form for the equation for the tangent line, and you have to understand how to substitute the given information about \(a,f(a),f'(a)\) into the general formula. Sometimes, this can actually be tricky. You will work on two such problems in this Class Drill.
Instructor: Show the solution to the Class Drill that the students just worked on. (See [Example 2] on pages 16 - 19 of the Notes from the Video for H25 .)
Instructor: Now we come to discussing shortcuts to finding derivatives. The shortcuts are called Derivative Rules. They are presented in Section 2.5 and Chapter 3 of the book, with homework coverage beginning in the Homework for Section 2.5.
Instructor: (on the board) Introduce the new notation for derivatives. (Notation that is presented on page 8 of the Notes from the Video for H29)
Our first derivative Rule is the Constant Function Rule.
The Constant Function Rule This rule is used for finding the derivative of a constant function.
Instructor: (on the board) Discuss why this rule makes sense, using the graph of a constant function \(f(x)=c\) and its derivative \(f'(x)=0\) to explain. (similar to discussion on pages 10,11 of the Notes from the Video for H29)
Our next derivative Rule is the Power Rule.
Power Rule This rule is used for finding the derivative of a power function.
Using the Power Rule can be complicated by the fact that functions are often not given in power function form. Using the Power Rule can be also complicated by calculations involving fractional exponents.
Furthermore, even though it is often necessary to rewrite functions in power function form in order to take a derivative, it will often happen that after finding a derivative, you will need to to rewrite the result in positive exponent form
Instructor: Present this first basic Example of Using the Power Rule with Integer Exponents
(See [Examples 2,3] on pages 13 - 15 of the Notes from the Video for H29 .)
Instructor: (on the board) Point out that the Power Rule can only be used on functions that are written in power function form. That is, functions of the form $$f(x)=x^p$$ Point out that to solve [Example 1](b) we had to find the derivative of \(\frac{1}{x^5}\) by first rewriting the function as a power function. Notice how not to do the derivative: $$\frac{d}{dx} \frac{1}{x^5} \neq \frac{1}{5x^4}$$ That is, $$\frac{d}{dx} \frac{1}{x^5} \neq \frac{1}{\frac{d}{dx}x^5} $$
Instructor: (on the board) We will now move on to more difficult examples showing the use of the Power Rule. In preparation for that, it will be useful to review a kind of calculation involving rational powers that frequently comes up in examples. It is a calculation that you might think that you would need a calculator to do, but in fact can be done easily without a calculator. (Instructor review pages 4 of the Notes from the Video for H29 .)
Instructor: If there is time, have students work on the following Class Drill:
Instructor: Show the solution to the Class Drill that the class just worked on. (See [Examples 4,6] on pages 15 - 17 of the Notes from the Video for H29 .)
Instructor: If there is time, have students work on the following Class Drill:
Instructor: Show the solution to the Class Drill that the class just worked on. (See [Examples 4,5,6] on pages 15 - 17 of the Notes from the Video for H29 .)
Quiz Q3 during the last part of the Fri Jun 7 class meeting
No Books, no Notes, no Calculators, no Phones, no Smart Watches
The quiz material is taken from the material covered in Section 2.4. See the List of Homework Assignments for links to the corresponding Instructional Videos.
Sections, Content, Homework, and Videos:
Instructor: We will learn only one more derivative Rule in Chapter 2.
The Sum and Constant Multiple Rule Rule If \(f(x)\) and \(g(x)\) are functions and \(a,b\) are constants, then $$\frac{d}{dx}\left(af(x)+bg(x)\right)=a\frac{d}{dx}f(x)+b\frac{d}{dx}g(x)$$ Using prime notation, we could write $$\left(af(x)+bg(x)\right)' = af'(x)+bg'(x)$$
Instructor [Example] Use the basic derivative rules to find the following derivative.
$$ \frac{d}{dx}( 5x^2-7x+3)$$Observe that this same derivative was the subject of a Class Drill during last Monday's meeting (Jun 3). On that day, the derivative was found used the Definition of the Derivative. That is, by evaluating the following limit: $$f'(x)=\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{h}$$ That method was much harder, but it gave the same result as using the Sum and Constant Multiple Rule Rule.
Using the Sum and Constant Multiple Rule can be complicated by the fact that functions are often not given in power function form. In two Class Drills you students will do examples of computing derivatives that require that the function be rewritten first, before taking the derivative.
Instructor: Have students work on the following Class Drill:
For the function $$f(x)=5+\frac{7}{x}$$ find \(f'(x)\) using the Derivative Rules.
Instructor: Show the solution to the Class Drill that the class just worked on. (See [Example 1] on page 3 of the Notes from the Video for H31 .)
Instructor: Observe that this same derivative was the subject of a Class Drill during last Wednesday's meeting (Jun 5). On that day, the derivative was found used the Definition of the Derivative. That method was much harder, but it gave the same result as using the Sum and Constant Multiple Rule Rule.
Instructor: Have students work on the following Class Drill:
For the function $$f(x)=5+7\sqrt{x}$$ find \(f'(x)\) using the Derivative Rules.
Instructor: Show the solution to the Class Drill that the class just worked on. (See [Example 2] on page 5 of the Notes from the Video for H31 .)
Instructor: Observe that this same derivative was the subject of a Class Drill during last Wednesday's meeting (Jun 5). On that day, the derivative was found used the Definition of the Derivative. That method was much harder, but it gave the same result as using the Sum and Constant Multiple Rule Rule.
Instructor: The skill of rewriting the function be first, before taking the derivative, will be one of the most important skills for the rest of the course. Please work on a Class Drill that will show you the general approach.
Instructor: Recall that we discussed the Tangent Line in a previous meeting. The Tangent Line is introduced on page 11 of the Notes from the Video for H25. The key thing is to remember from the definition is the two properties of the tangent line.
The line tangent to the graph of \(f(x)\) at \(x=a\) has the following two properties
Knowing those two properties of the tangent line, we are able to write down a general form for the equation for the tangent line. It is discussed on page 13 of the Notes from the Video for H25. The general form (as discussed in the video notes) is
$$(y-f(a))=f'(a)(x-a)$$The general approach to finding the equation of the tangent line is
Some simple problems actually give you information about \(a,f(a),f'(a)\) and ask you to give the equation of the tangent line. These problems are simpler, because you don't have to do the computation of the parts \(f(a),f'(a)\). They are given to you. But you still have to know the general form for the equation for the tangent line, and you have to understand how to substitute the given information about \(a,f(a),f'(a)\) into the general formula.
Instructor: Have students work on the following Class Drill:
Suppose that a function \(f(x)\) has \(f(3)=5\) and \(f'(3)=-7\).
Instructor: Show the solution to the Class Drill that the class just worked on. (To prepare for this presentation, study pages 11 - 14 of the Notes from the Video for H25 .)
Instructor: Here is a much longer example, involving a variety of types of questions that can be asked about tangent lines.
(Instructor present this example. For a similar example, see [Example 2] on pages 7 - 11 of the notes for Video 32.)
Instructor [Example #1]: Let \(f(x)=x^{3}+3x^2-9x+5=(x+5)(x-1)^2\)
Instructor Ask Question #1 for the Class: Frick and Frack have been asked the following:
They are arguing about the result.
Frick and Frack are both wrong!
Frick says that the derivative is the slope of the tangent line. But this is not correct. The slope of the tangent line is a number. The derivative is a function, not a number. (The derivative is a function that can be used to find the number that is the slope of the tangent line.)
Frack is also wrong. Frack computed the slope of a secant line.
The correct procedure to find the slope of the line tangent to the graph of \(f(x)=x^3\) at \(x=5\) is as follows.
Step 1: Find \(f'(x)\). The result is
$$ \frac{d}{dx}x^3=3x^{3-1}=3x^2$$Step 2: Substitute \(x=5\) into \(f'(x)\) to get \(m=f'(5)\). The result is
$$ m=f'(5)=3(5)^2=3\cdot25=75$$Instructor Ask Question #2 for the Class: Wacky Jack has been asked the following:
Their answer was $$y=2x^3-5x^2+4x-11$$ Is Wacky Jack's answer correct?
At first, you might think that of course one would need more information before being able to say whether Wacky Jack's answer is right or wrong. But in fact, it is easy to see immediately that Wacky Jack's answer is incorrect.
The key is to remember that Wacky Jack was asked to find the equation of a line. That means that his result must be in the form $$y=mx+b$$ where \(m\) and \(b\) are numbers. Since Wacky Jack's answer is not in that form, his answer is incorrect.
This example illustrates one kind of quick check on problems involving finding the equation of a tangent line. You will encounter problems of that sort where the calculations get quite messy. But the end result should always be an equation of the form \(y=mx+b\).
Instructor: If there is time, discuss another topic:
Instructor ask Question #3 for the Class: Suppose that an object is moving along a straight track with position function \(f(x)\), where \(x\) is the time in seconds and \(f(x)\) is the position in meters at time \(x\).
Recall that the quantity $$ \frac{f(17)-f(13)}{17-13}$$ is called the average rate of change of \(f\) from \(x=13\) to \(x=17\).
And the quantity $$ f'(8)$$ is called the instantaneous rate of change of \(f\) at \(x=8\).
In the special case that the variable \(x\) represents time and the function \(f(x)\) represents the position, at time \(x\), of an object moving in one dimension, the quantity $$ \frac{f(17)-f(13)}{17-13}$$ is called the average velocity of the object from time \(x=13\) to time \(x=17\).
And the quantity $$ f'(8)$$ is called the instantaneous velocity of the object at time \(x=8\).
The units of both of these velocities will be the ratio $$\frac{units \ of \ position}{units \ of \ time}$$ So in our particular example, the units will be meters per second.
To understand why these are the units, remember that the quantities are slopes of lines on a graph of \(f(x)\) -vs- \(x\). The slope of a line is computed by the ratio $$m=\frac{\Delta y}{\Delta x}$$ If the \(x\) and \(y\) quantities have units attached, then the units of the slope will work out to be $$m=\frac{units \ of \ y}{units \ of \ x}$$ In the special case of position and velocity, the units will be $$m=\frac{units \ of \ f(x)}{units \ of \ x}$$ That is $$m=\frac{units \ of \ position}{units \ of \ time}$$
Instructor: If there is time, discuss another topic:
Instructor: Remember that in Mathematics, an Application Problem involves using math to solve some real world problem. An important part of an application problem is interpreting the result. What this means is the following: In an application problem, one uses functions and equations to model an actual real-world situation. One then does abstract mathematical calculations to reach some abstract mathematical result. It is important to write a clear conclusion that explains what the abstract mathematical result tells us about the real-world situation. This is what is meant by interpreting the result.
In Calculus, an Application Problem often uses the important fact that the following quantities are equal.
Interpreting the result will often involve explaining something about a rate of change.
Here is an example that asks the student to interpret some results.
Instructor [Example #2] (See pages 5-8 of the Notes from the Video for H33 for a similar example.)
A company introduced a new Gas Powered Back Scratcher. Total sales are described by the function \(S(t)\), where \(t\) is the time in months since the new Gas Powered Back Scratcher was introduced and \(S(t)\) is the total sales (in millions of dollars) at time \(t\).
Instructor: So far, when we have discussed applications of Calculus, they have been applications of a sort that one would see in any Calculus course. Namely, the applications have been about the important fact that the following quantities are equal.
But MATH 1350, in addition to being a Survey of Calculus course, also fills the role of being the Business Calculus course for Ohio University. In that role, the course will consider applications of Calculus that have to do with Business.
In the Video for H34, you were introduced to some Business Terminology, namely Demand and Cost.
Instructor Project page 2 of the Notes from the Video for H34.
Homework H34 is a very short homework assignment about computing Cost. The homework set contains only one problem, because the MyLab system contains only one problem of the sort. But the Video for H34 presents a more thorough example about computing cost. You will work on a Class Drill involving a similar example, which we will call the [Bicycle Example].
In the Video for H35, you were introduced to some more Business Terminology, namely Revenue and Profit, and the concept of Marginal Quantities.
Remember that a Marginal Quantity is simply the Derivative of a Quantity. For example:
$$Marginal \ \ Cost = Derivative \ \ of \ \ Cost = C'(x)$$In the Video for H36, you learned about using Marginal Quantities to Estimate Change in Quantities . The general idea is summarized as follows:
Using Marginal Quantities to Approximate Change in Quantities
$$ \begin{eqnarray} Exact \ Change &\approx& Approximate \ Change \\ \underbrace{\Delta Q}_{Exact \\ Change} = \underbrace{Q(x_0+1) - Q(x_0)}_{Exact \\ Change} &\approx& \underbrace{Q'(x_0)}_{Approximate \\ Change} \\ \end{eqnarray} $$In the following Class Drill, you will do an example called the [Bicycle Example]. In the example, you will first compute an Exact Change in a Quantity. Then you will compute a Marginal Quantity and use it to find an Approximate Change in a the same quantity.
Instructor: Have students work on the following Class Drill:
The total cost of producing \(x\) bicycles is
$$C(x)=10,000+150x-0.2x^2 \ \ dollars$$(A) What is the cost of producing a batch of \(140\) bicycles? (Show all details clearly and simplify your answer.)
(B) What is the cost of producing a batch of \(141\) bicycles? (Show all details clearly and simplify your answer.)
(C) If batch size changes from \(x=140\) bicycles to \(x=141\) bicycles, what will be the change in cost of producing a batch of bicycles? That is, if \(x=140\) and \(\Delta x = 1 \), what is \(\Delta C\)? (exact value) (Show all details clearly and simplify your answer.) This quantity is an Exact Change in Cost. (The book calls this quantity the cost of producing the 141st bicycle.)
(D) Find the Marginal Cost. (Show all details clearly and simplify your answer.)
(Hint: Since you are not told what method to use to find the Marginal Cost, use the easy method, involving the Derivative Rules, rather than the hard method, involving the Definition of the Derivative.)
(E) If batch size changes from \(x=140\) bicycles to \(x=141\) bicycles, use the marginal cost function to find an approximate value for the change in cost of producing a batch of bicycles. That is, use the Marginal Cost Function to find an approximation for \(\Delta C\). (Show all details clearly and simplify your answer.) The book calls this quantity the approximate cost of producing the 141st bicycle.)
Instructor: Show the solution to the Class Drill that the class just worked on. (For Reference, see the [Example 1] on page 3 of the Notes from the Video for H34 and the [Example 1] on page 10 of the Notes from the Video for H36.)
Instructor: Notice that the approximate result found in (E) is very close to the exact result found in (C).
Instructor: In the Video for H35, you were introduced to Revenue.
(Instructor Project page 2 of the Notes from the Video for H35.)
Not much was said there about Revenue except that \(R(x)\) is the amount of money that comes in from the sale of a batch of \(x\) items.
In the Video for H36, the concept of Revenue is developed further. Using the simplifying assumption that all the items in a batch of items are sold for the same selling price, we can introduce a new business term: price.
(Instructor Project page 13 of the Notes from the Video for H36. Discuss the terms Price, Price Demand Equation, and Price Function. Also discuss the relationship between Price and Revenue shown on that page.)
You will explore Price and Revenue in an extended example in a Class Drill.
Instructor: Have students work on the following Class Drill:
A company makes hoverboards, a very dangerous toy that kids would not ride if they had a lick of sense. The price demand equation is $$x=6,000-30p$$ where \(p\) is the selling price of a hoverboard, in dollars, and \(x\) is the number of hoverboards that will sell at that price.
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see [Example 2] on page 14 of the Notes from the Video for H36 .)
Exam X1 lasts the full duration of the Fri Jun 14 class meeting
No Books, no Notes, no Calculators, no Phones, no Smart Watches
The exam material is taken from the material covered in Chapter 2. See the List of Homework Assignments for links to the corresponding Instructional Videos.
Sections, Content, Homework, and Videos:
Instructor: Book Section 3.1 begins with an introduction to the number \( e \) and the function \( e^{(x)} \). That introduction involves a lot of detailed discussion of limits that is better left to the video. (See the Video for H37 and its accompanying notes.) But it is useful to discuss the graphs of basic exponential functions.
Instructor: Draw graphs of \( y=2^{(x)} \) and \( y=e^{(x)} \) \( y=3^{(x)} \) together on one set of axes. Point out that the graph of \( y=e^{(x)} \) is always between the other two because \( 2 \lt e \lt 3 \).)
Questions for Class: What are some important properties of these graphs? (Instructor: see page 11 of the Notes from the Video for H37 for a discussion of this topic.)
Instructor: Book Section 3.1 also explores ways of computing interest on a bank account. Three kinds of bank account interest are discussed:
(Instructor: See page 2 of the Notes from the Video for H38 for a discussion of this topic.)
Instructor: Introduce how an account with Simple Interest works. Write the formula for the balance of an account with Simple Interest, and draw its graph. Discuss its important features:
Instructor do this [Example]: Suppose that $1000 is deposited into a bank account with \(5\%\) simple interest. What will be the balance after 10 years?
(Instructor: See page 5 of the Notes from the Video for H38 for a discussion of this topic.)
Instructor: Introduce how an account with Periodically-Compounded Interest works. Write the formula for the balance of an account with Periodically-Compounded Interest, and draw its graph. Discuss its important features:
Instructor do this [Example]: Suppose that $1000 is deposited into a bank account with \(5\%\) interest compounded monthly. What will be the balance after 10 years?
(Instructor: See page 11 in the Notes from the Video for H38 for a discussion of this topic.)
Instructor: Introduce how an account with Continuously-Compounded Interest works. Write the formula for the balance of an account with Continuously-Compounded Interest, and draw its graph. Explain that there is discussion of where this formula comes from in the Video for H38.
Instructor: The equation \(A=Pe^{(rt)}\) involves the four letters \(A,P,r,t\) and is solved for \(A\). The equation can be solved for each of the other letters \(P,r,t\). This is useful in solving a variety of problems that you will encounter in your homework.
Instructor: Show how to solve that equation for the other variables.
Here are examples of four kinds of problems whose solutions involve solving the equation \(A=Pe^{(rt)}\) for one of the letters \(P,r,t\):
You will have problems of these types to do in your Homework H38. Examples of three of the four types are presented on pages 12 - 14 of the Notes from the Video for H38. Observe the style of the solutions. They always follow this format:
we'll see two basic examples of these types of problems in Class Drills.
Instructor: Have students work in groups of 2 or 3 on the following Class Drill:
Suppose that \($2000\) is deposited into an account with \(5\%\) interest compounded continuously. How long after the initial deposit will the balance have grown to \($3000\)? (Give an exact answer, in symbols, then a decimal approximation. Show all details clearly.)
Student #2 Presentation CP2: Show the solution to the Class Drill that the class just worked on. (To prepare for this presentation, study pages 12 - 14 of the Notes from the Video for H38 .)
Instructor: Have students work on the following Class Drill:
If you want an account with continuously compounded interest to double in 15 years, what interest rate will you need? (The book would ask at what nominal rate compounded continuously must the money be invested?) (Give an exact answer, in symbols, then a decimal approximation. Show all details clearly.)
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see pages 12 - 14 of the Notes from the Video for H38 .)
Instructor: In this section, we will learn how to find the derivatives of exponential functions. Before discussing that, however, it is worthwhile to note the distinctions between exponential functions and power functions. Both types of functions have a base and an exponent. But there is an important difference: which parts are constant and which parts are variable.
In a power function, $$f(x)=x^p$$ the base is a variable and the exponent is a number.
In an exponential function, $$f(x)=e^{(x)} \ \text{ or } \ b^{(x)} \ \text{ or } \ e^{(kx)} \ \text{ or } \ b^{(kx)}$$ the base is a number and the exponent is a variable (or an expression involving a variable).
Recall the Power Rule for derivatives of power functions:
$$ \frac{d}{dx} x^n = nx^{(n-1)} $$In book Section 3.2 and in the MATH 1350 Videos, we see the introduction of Exponential Function Rules #1, #2, #3, for finding derivatives of exponential functions:
$$ \frac{d}{dx} e^{(x)} = e^{(x)}$$ $$ \frac{d}{dx} e^{(kx)} = ke^{(kx)}$$ $$ \frac{d}{dx} b^{(x)} = b^{(x)}\ln{(b)}$$We now have four rules for finding derivatives of expressions that involve exponents. When taking such a derivative, it is important to use the correct rule!
In your Homework for Section 3.2, you are asked to find various derivatives involving exponential functions, power functions, and constant functions. To succeed in these problems, you have to figure out which rule to use. Barsamian does similar examples in the Video for H40. (Link to Notes for that Video)
Instructor: Do this [Example: Computing Derivatives of Expressions that have Exponents].
Find the following derivatives. Use clear notation and indicate which rule you used in each step.
$$(a) \ \frac{d}{dx} 7x = $$ $$(b) \ \frac{d}{dx} 7x^3 = $$ $$(c) \ \frac{d}{dx} 7e^x = $$ $$(d) \ \frac{d}{dx} 7e^{13} = $$ $$(e) \ \frac{d}{dx} 7\cdot 13^x = $$In your Homework for Section 3.2, you are asked to solve a tangent line problem for a function \(f(x)\) that has a term that is an exponential function. Barsamian does a similar example in the Video for H41. (Link to Notes for that Video)
Instructor: Do this [Example: Computing a Tangent Line Equation for an Exponential Function].
For the function $$f(x)=3e^{(x)}-5x$$
Instructor: Recall something that was first discussed during the Friday May 31 meeting and has been discussed in meetings since, and that is discussed throughout the Videos:
An important concept for the second month of MATH 1350 is the relationship between the derivative, the tangent line, and rate of change:
Sometimes you will get questions that require you to understand the connection between those three quantities.
In your Homework for Section 3.2, you are asked to answer two questions about the instantaneous rate of change of the value of an investment that is earning continously-compounded interest. Barsamian does a similar example in the Video for H41. Realize that to solve this problem, you need to recognize the connection between the three quantities mentioned above.
Instructor: Have students work on the following Class Drill:
An Investment of \($5000\) earns interest at an annual rate of \(4 \% \) compounded continously.
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see [Examples 2 and 3] in the Notes from the Video for H41 .)
Sections, Content, Homework, and Videos:
Instructor: Today, we'll be discussing logarithmic functions and their derivatives. We start by reviewing the graph of the simplest logarithmic function, the function
$$ y=\ln{(x)} $$See the Notes from the Video for H43, and discuss the following questions:
We find the derivative of the natural logarithm function \(y = \ln{(x)} \) by using a rather surprising new derivative rule:
Logarithmic Function Rule #1: $$\frac{d}{dx}\ln{(x)} = \frac{1}{x} $$
We can consider why Logarithmic Function Rule #1 makes sense by projecting and discussing page 7 of the Notes from the Video for H43.)
We find the derivative of the more general base \(b\) logarithm function \(y = \log_b{(x)} \) by using a slight variation of the above rule:
Logarithmic Function Rule #2: $$ \frac{d}{dx}\log_b{(x)} = \frac{1}{x\cdot\ln{(b)}} $$
Instructor: It is important to realize that both of the new Logarithmic Function Rules only work when the thing inside the logarithm is just the variable. What happens when the thing inside the logarithm is an expression that is not simply the variable? You'll tackle this issue in a Class Drill.
Derivatives with just a single item inside the logarithm
Derivatives with an expression inside the logarithm
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see the [Examples] on page 9 of the Notes from the Video for H43 .)
Instructor: In your homework, you are asked to find the equations of lines tangent to graphs of functions involving exponential functions (in H41) and logarithmic functions (H44). These might at first look like very hard problems.
But understand that one part of the difficulty involves using rules of exponents and logarithms, which are rules from high school that you may have forgotten but that should at least look familiar to you and that will come back to you with some practice.
Another bit of difficulty in the tangent line problems is that you have to find derivatives. But the only derivatives involved in Homeworks H41 and H44 are the very basic rules:
A third bit of difficulty in the tangent line problems is understanding what is being asked for and knowing how to structure your solution to the problem. That is worth reviewing here.
Recall that the line tangent to the graph of \(f(x)\) at \(x=a\) has the following two properties:
Knowing those two properties of the tangent line, we are able to write down a general point slope form for the equation for the tangent line.
$$(y-f(a))=f'(a)(x-a)$$The general approach to finding the equation of the tangent line is
Although problems about finding tangent line equations can seem daunting, remember that the general form of the solution is always the same, and that often, the underlying details involve old concepts from high school or basic derivatives from calculus.
Instructor: For the rest of the meeting, you will work on two Class Drills involving tangent lines.
Find the equation of the line tangent to the graph of \( f(x)=5e^{(x)}-7x\) at \(x=1\).
(Hint: Remember that you should start by building the point slope form of the equation of the tangent line. $$\left(y-f(a)\right)=f'(a)\left(x-a\right)$$ After finding the parts \(a\),\(f(a)\),\(f'(a)\) and using them to build the formula, you should convert your formula to slope intercept form. Simplify your answer.)
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see MyLab Homework H41 problem #1 and [Example 1] on page 3 of the Notes from the Video for H41 .)
Instructor: If there is time, have students do another Class Drill:
(This Class Drill is based on one of the problems from the Homework for Section 3.2.)
Let
$$f(x)=7+\ln{(x^5)}$$Instructor: Show the solution to the Class Drill that the class just worked on. (See the [Example] on page 3 of the Notes from the Video for H44 .)
Instructor: We'll start today's meeting by discussing Products of Functions. That is, functions of the form $$f(x)=g(x)\cdot h(x)$$ A natural question is:
There is an obvious way that might occur to you, but the obvious way is WRONG!! $$ \frac{d}{dx}\left( g(x) \cdot h(x) \right) \neq \left( \frac{d}{dx}g(x) \right)\cdot \left( \frac{d}{dx} h(x) \right) $$ That is,
The correct way to find the derivative of a product is to use the Product Rule.
$$ \frac{d}{dx}\left( g(x) \cdot h(x) \right) = \left( \frac{d}{dx}g(x) \right)\cdot h(x) + g(x)\cdot \left( \frac{d}{dx} h(x) \right) $$Using prime notation, we would write the Product Rule this way:
$$ \left( g(x) \cdot h(x) \right)' = g'(x) \cdot h(x) + g(x)\cdot h'(x) $$Instructor : Do this Example] (Similar to MyLab H45 Problem #4)
For the function
$$f(x)=e^{(x)}\left(7x^3-5x^2+13\right)$$
The class will do another basic example involving the Product Rule as a Class Drill.
For the function $$f(x)=3x^5\ln{(x)}$$
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see [Example 4] on page 9 of the Notes from the Video for H45 .)
Instructor: Next we'll discuss Quotients of Functions. That is, functions of the form $$f(x)=\frac{top(x)}{bottom(x)}$$ A natural question is:
There is an obvious way that might occur to you, but the obvious way is WRONG!! $$\frac{d}{dx}\left(\frac{top(x)}{bottom(x)}\right) \neq \frac{\frac{d}{dx}top(x)}{\frac{d}{dx}bottom(x)} $$ That is,
The correct way to find the derivative of a quotient is to use the Quotient Rule.
$$ \frac{d}{dx}\left(\frac{top(x)}{bottom(x)}\right) = \frac{\left( \frac{d}{dx}top(x) \right)\cdot bottom(x) - top(x)\cdot \left( \frac{d}{dx} bottom(x) \right)}{(bottom(x))^2} $$Using prime notation, we would write the Quotient Rule this way:
$$ \left(\frac{top(x)}{bottom(x)}\right)' = \frac{top'(x) \cdot bottom(x) - top(x)\cdot bottom'(x)}{(bottom(x))^2} $$Instructor : Do this [Example] (Similar to one of the exercises on the Homework for Section 3.3)
For the function
$$f(x)=\frac{e^{(x)}}{7x^5+3}$$
Instructor: The Quotient Rule is a very messy derivative rule, and there are lots of opportunities to make mistakes when using it. Therefore, it is important to recognize situations when the quotient rule is unnecessary. Sometimes a function that is presented as a quotient can be rewritten in a way that it is not a quotient. Then, simpler derivative rules can be used to find the derivative.
Instructor: Do this [Example] involving the Very Important Trick.
For the function $$f(x)=\frac{3}{x^5}$$ find \(f'(x)\) using two different methods.
Observe that in the [Example], both methods give the same result, but using the Quotient Rule involves more work and presents more opportunities to make mistakes!
The important conclusion from the [Example] is
When finding the derivative of a function, one should always check to see if it is possible convert the function to power function form before taking the derivative.
The class will do another problem involving the Very Important Trick in a Class Drill.
For the function $$ y=\frac{2x^5-4x^3+2x}{x^3} $$ find \(f'(x)\) using two different methods.
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see the Notes from the Video for H47 .)
Quiz Q4 during the last part of the Jun 26 class meeting
No Books, no Notes, no Calculators, no Phones, no Smart Watches
The quiz material is taken from the material covered in book Sections 3.1 and 3.2. See the List of Homework Assignments for links to the corresponding Instructional Videos.
Instructor: Last Wednesday, we discussed the Quotient Rule.
$$ \frac{d}{dx}\left(\frac{top(x)}{bottom(x)}\right) = \frac{\left( \frac{d}{dx}top(x) \right)\cdot bottom(x) - top(x)\cdot \left( \frac{d}{dx} bottom(x) \right)}{(bottom(x))^2} $$Using prime notation, we would write the Quotient Rule this way:
$$ \left(\frac{top(x)}{bottom(x)}\right)' = \frac{top'(x) \cdot bottom(x) - top(x)\cdot bottom'(x)}{(bottom(x))^2} $$We'll start today's meeting with a problem involving finding the equation for the tangent line for function that is a quotient. You'll solve the problem as a Class Drill.
Let \(f(x)\) be the function $$f(x)=\frac{50x}{x+4}$$ Find the equation of the line tangent to the graph of \(f(x)\) at \(x=6\). Convert your equation to slope intercept form.
Student #9 Presentation CP2: Show the solution to the Class Drill that the class just worked on. (To prepare for this presentation, study MyLab Homework H48 problem #1 and [Example 1] in the Notes from the Video for H48 .)
Instructor: An important concept for Sections 2.4, 2.5, 3.2, 3.3, 3.4 is the relationship between the derivative, the tangent line, and rate of change. In the videos, you have seen discussed the idea that the following three quantities are all equal:
In the following [Example], an Application problem is posed. Questions (a), and (b) are about calculating certain abstract mathematical quantities. Question (c) asks the reader to interpret those abstract results.
[Example] Sales of a game are described by the function
$$ S(t)=\frac{150t}{t+6} $$
where \(t\) is the time (in months) since the game was introduced
and \(S(t)\) is the total sales (in thousands of games) at time \(t\).
Observe that there are three Questions. Questions (a) and (b) involve calculations. In a HW, Quiz, or Exam question, you would have to do these calculations. But here in this example, I've provided answers to those parts. You just have to answer (c).
Remark: Notice that to answer Question (c), we had to make the connection that the following two quantities are equal:
Sections, Content, Homework, and Videos:
Instructor: Compositions of Functions are functions of the form $$f(x)=outer\left(inner(x)\right)$$ Another name for this kind of function could be Nested Functions.
One finds the derivative of a nested function by using the Chain Rule.
The Chain Rule (Used for finding the derivative of a composition of functions. That is, nested functions.)
Two Equation Form:
$$\text{If } \ f(x)=outer(inner(x)), \ \ \text{then } \ \ f'(x)=outer'(inner(x))\cdot inner'(x)$$Single Equation Form:
$$\frac{d}{dx}outer(inner(x))=outer'(inner(x))\cdot inner'(x)$$Notice that the presentation of the Chain Rule in the MATH 1350 Videos uses the terminology of inner function and outer function. And more specifically, notice that the inner function always has a variable inside, while the outer function is often expressed as an empty function, with empty parentheses not holding any variable. In the course of using the Chain Rule, the derivatives of these inner and outer functions are used, and the derivatives have the same type of variable as the original. In other words, you will be working with the following four functions:
$$inner(x) \\ inner'(x) \\ outer( \ \ ) \\ outer'( \ \ )$$The use of empty functions for the outer function and its derivative is central to the use of the Chain Rule in the MATH 1350 Videos. It is worthwhile for you to learn to use that kind of notation.
In this second part of the meeting, we’ll three see examples involving using the Chain Rule when the outer function is a power function. The first two of these examples will be done by the instructor; the third will be done as Class Drill.
Instructor: Do this [Chain Rule Example #1]: Use the Chain Rule to find the derivative of $$f(x)=3\left(6x^2-4x+5\right)^4$$ Be sure to use the terminology and notation of the inner function and outer function, where the outer function is an empty function. (For Reference, see MyLab Homework H49 problem #1 and [Example 1] on page 7 of the Notes from the Video for H49 .)
Instructor: Do this [Chain Rule Example #2]: Use the Chain Rule to find the derivative of $$f(x)=\frac{3}{\left(6x^2-4x+5\right)^4}$$ Be sure to use the terminology and notation of the inner function and outer function, where the outer function is an empty function. (For Reference, see MyLab Homework H49 problem #3 and [Example 2] on page 8 of the Notes from the Video for H49 .)
The next Chain Rule example will be done as a Class Drill.
Use the Chain Rule to find the derivative of $$f(x)=4\sqrt{6x^2-4x+5}$$ Be sure to use the terminology and notation of the inner function and outer function, where the outer function is an empty function.
Instructor: Show the solution to the Class Drill that the class just worked on. (For Reference, see [Example 3] on page 9 of the Notes from the Video for H49 .)
So far, you have seen three examples where the Chain Rule is used to find derivatives of functions where the outer function is a power function. While no Chain Rule problem is easy, it is important to understand that if one is careful to acknowledge the form of a Chain Rule problem, then at least all Chain Rule problems will begin to look familiar. Indeed, if we look at the three examples that start on page 7 in the Notes from the Video for H49, we see that they all have identical form! Only the details of the derivative of the outer function, and the details of the simplifying, differ.
In this third part of the meeting, we’ll see two examples involving using the Chain Rule when the outer function is an exponential function. The first of these examples will be done by the instructor; the second will be done as Class Drill.
We start with a chain rule problem that proves a result that you have seen before, as one of the derivative rules.
Instructor: Use the Chain Rule to prove the following derivative rule: $$\frac{d}{dx}e^{\left(kx\right)}=ke^{\left(kx\right)}$$ Be sure to use the terminology and notation of the inner function and outer function, where the outer function is an empty function.
In the following Class Drill, you students will do a longer example that starts by using the Chain Rule to find the derivative of a function where the outer function is an exponental function.
for the function $$f(x)=e^{\left(6x^2-4x+5\right)}$$
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see [Example 2] on page 6 of the Notes from the Video for H50 .)
Instructor: on Monday, we discussed the Chain Rule.
The Chain Rule (Used for finding the derivative of a composition of functions. That is, nested functions.)
Two Equation Form:
$$\text{If } \ f(x)=outer(inner(x)), \ \ \text{then } \ \ f'(x)=outer'(inner(x))\cdot inner'(x)$$Single Equation Form:
$$\frac{d}{dx}outer(inner(x))=outer'(inner(x))\cdot inner'(x)$$In Monday's meeting, you saw three examples where the chain rule was used to find derivatives of functions where the outer function is a power function.
And you saw two examples where the chain rule was used to find derivatives of functions where the outer function is an exponential function.
In the first part of today's meeting, the class will work on a Class Drill involving using the Chain Rule to find the derivative of a nested function where the outer function is an logarithmic function
for the function $$f(x)=\ln\left(2x^2-8x+10\right)$$ use the Chain Rule to find \(f'(x)\). Be sure to use the terminology and notation of the inner function and outer function, where the outer function is an empty function.
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see [Example 3] on page 11 of the Notes from the Video for H50 .)
Instructor: We have seen a number of examples that included questions about slopes of tangent lines and about horizontal tangent lines. It is worthwhile to pause here and review the slopes of tangent lines.
[Example] Answer the following questions about the function \(f(x)=2x^3-3x^2-12x+5\).
Solution: These questions are all about the important fact that the following three things are all equal:
The strategy for solving problems (a),(b) is therefore
Those calculations are straightforward.
$$\begin{eqnarray} f'(x)&=&\frac{d}{dx} \left(2x^3-3x^2-12x+5\right) = \cdots = 6x^2-6x-12 \\ (a) \ m &=& f'(3) = 6(3)^2-6(3)-12=54-27-12=15 \\ (b) \ m &=& f'(0) = 6(0)^2-6(0)-12=-12 \end{eqnarray} $$The solution of (c) is more subtle. The key is to remember the following important fact:
Horizontal lines have slope \(m=0\)
The strategy for solving (c) is therefore
We already found \(f'(x)=6x^2-6x-12\). Setting \( f'(x)=0 \) and solving for \(x\) is straightforward. It helps to turn the equation around
$$0=f'(x)=6x^2-6x-12=6\left(x^2-x-2\right)=6(x+1)(x-2)$$The solutions to this equation are \(x=-1\) and \(x=2\). So those are the \(x\) values where the graph of \(f(x)\) has a horizontal tangent line. This is believable, because the graph of \(f(x)\) will be a cubic shape, with two turning points. Now we see that the turning points will be at \(x=-1\) and \(x=2\).
End of [Example]
An important takeaway from the example above is the important distinction between two calculations involving \(f'(x)\) and the number \(0\).
Question: When is a fraction equal to zero?
Answer: When the numerator equals zero and the denominator is NOT zero.
Therefore, solving equations of the form $$\frac{numerator(x)}{denominator(x)}=0$$ involves finding the \(x\) values that cause \(numerator(x)=0\), and then checking to be sure that for those \(x\) values, \(denominator(x) \neq 0\).
This idea came up in a few presentations and examples in this and the last couple of meetings.
Now, the class will work on a Class Drill involving Tangent Lines for the logarithmic function that was studied in the earlier Class Drill
Earlier in today’s meeting, you found that for the function $$f(x)=\ln\left(2x^2-8x+10\right)$$ the derivative is $$f’(x)=\frac{4x-8}{\left(2x^2-8x+10\right)}$$
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see [Example 3] on page 11 of the Notes from the Video for H50 .)
Quiz Q5 during the last part of the Wed Jul 3 class meeting
No Books, no Notes, no Calculators, no Phones, no Smart Watches
The quiz material is taken from the material covered in book Sections 3.3 and 3.4. See the List of Homework Assignments for links to the corresponding Instructional Videos.
Instructor: In Chapter 2, starting in Section 2.4 of the book, you learned about the Derivative. In Chapter 3, you learned how to use the Derivative Rules to find the derivative of a variety of kinds of functions. During the weeks of the course that you were learning about the derivative, an important concept was the fact that the following three quantitites are all equal:
In Chapter 4, you will learn to use the derivative in more ways. In the first few sections, you will use the derivative in a more thorough analysis of the formula for \(f(x)\) to determine more about the behavior of the graph of \(f(x)\). Section 4.1 is about using the derivative, \(f'(x)\), to determine the increasing & decreasing and max & min behavior of the graph of \(f(x)\).
An important concept in Section 4.1 (and beyond) is the distinction between positive & negative and increasing & decreasing. These words are used in various ways in common English, but they have particular definitions in Math.
Instructor: In our first Class Drill for today, you will practice drawing graphs with instructions that use the terminology of positive & negative and increasing & decreasing.
Draw four examples (four separate graphs) of functions \(f(x)\) on the domain \(1 \lt x \lt 5\)
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see Notes from the Video for H53 .)
Instructor: In the Video for H53, Barsamian presents this important correspondence:
Here is another short Class Drill that will give you practice using the correspondence just introduced.
Draw four examples (four separate graphs) of functions \(f(x)\) on the domain \(1 \lt x \lt 5\)
Instructor: In the Homework for Section 4.1, you work with functions that are described by a formula, not by a graph. You analyze the formula for \(f(x)\) and you also analyze the formula for \(f'(x)\) in order to determine certain things about \(f(x)\). Here is the Strategy for analyzing \(f(x)\) and \(f'(x)\):
Question for the Class: What is a partition number? Why are they part of the strategies described above? That is, how are partition numbers used?
Answer: Recall from Section 2.3 (about Continuity) the definiton of partition number.
A partition number for a function \(f\) is an \(x\) value where \(f\) is discontinuous or \(f(x)=0\).
Partion numbers for \(f\) are significant because on the intervals between the partition numbers for \(f\), the sign of the function \(f\) does not change.
There is a slight variation of the definition of partition number when we are talking about partition numbers for \(f'(x)\)
A partition number for \(f'\) is an \(x\) value where \(f'\) is undefined or \(f'(x)=0\).
Partion numbers for \(f'\) are significant because on the intervals between the partition numbers for \(f'\), the sign of \(f'\) does not change. This in turn means that the increasing/decreasing behavior of \(f\) does not change.
Instructor: in Video for H21, Barsamian first discussed the Procedure for Constructing Sign Charts for a function \(f(x)\). His procedure was basically the book's procedure, but with some modifications. Here is Barsamian's version of the procedure (with his modifications shown in bold):
Procedure: Constructing Sign Charts for a function \(f(x)\)
Given a function \(f(x)\),
The Procedure for Constructing Sign Charts for a derivative \(f'(x)\) is basically the same, but there are some slight differences. It is simple enough to show that slightly dissimilar procedure:
Procedure: Constructing Sign Charts for \(f'(x)\)
Given a function \(f(x)\),
Instructor: In our final Class Drill for today, you will construct two sign charts: A sign chart for \(f(x)\) and another sign chart for \(f'(x)\). You will use these sign charts to determine behavior of the graph of \(f(x)\).
Let \(f(x) = x^2-8x+15 \).
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see [Example 1] on page 5 of the Notes from the Video for H54 .)
Instructor: Notice that in Barsamian's version of the Procedure for Constructing Sign Charts, his Step 4 is
Now that we have seen the Presentation of Student #12, we see why that label on the sign chart is so important. We saw that in the Presentation of Student #12, two sign charts were made. These two sign charts were used for different things:
That's why it is so important to label the sign charts. Depending on what a sign chart is the sign chart for, it will get used for different things.
Instructor Present this much harder [Example]: (Similar to [Example 2] on page 10 of the Notes from the Video for H54) Let \(f(x) = x^4-4x^3 \).
Sections, Content, Homework, and Videos:
Instructor: Remember that Section 4.1 is about using the derivative to determine the increasing & decreasing and max & min behavior of the graph of \(f(x)\).
So far, we have discussed techniques for determining the increasing & decreasing behavior of \(f(x)\).
On Friday, we discussed the important correspondence between sign behavior of \(f'(x)\) on an interval \( (a,b) \) and behavior of the graph of \( f(x) \) on the interval \( (a,b) \).
Also on Friday, we talked about partition numbers for a function \(f(x)\) and for its derivative \(f'(x)\). These were discussed earlier in this meeting. You can scroll up and see the earlier discussion.
Today, we'll discuss techniques for determining the max & min behavior of \(f(x)\).
An important tool in determining the max & min behavior of \(f(x)\) is what are called critical numbers. You learned about critical numbers for a function \(f(x)\) on page 6 of the Video for Homework 55.
For a polynomial function \(f(x)\), finding the partition numbers for \(f'(x)\) and the critical numbers for \(f(x)\) is pretty straightforward. But for a function \(f(x)\) that is not a polynomial, it can be tricky. In your first class drill, you will work on an example where it is a little tricky.
For the function $$f(x)=x+\frac{16}{x}$$ Show how to find the partition numbers for \(f'(x)\) and the critical numbers for \(f(x)\).
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see [Example 5] in the Video for Homework 56 .)
Instructor: On page 5 of the Notes for the Video for H56, you saw the definitions of Local Maximum and Local Minimum. (Project the notes from the video and show them the definitions.)
Then, on page 7 of the same video, you learned about the First-Derivative Test for Local Extrema. (Project the notes from the video and show them the test.)
In the next class drill, you will practice using the First Derivative Test in an example where some helpful information about \(f(x)\) and \(f'(x)\) is given. That information will allow you to immediately use the First Derivative Test. (In harder problems, you will have to analyze both \(f(x)\) and \(f'(x)\) to determine the information that will allow you to use the First Derivative Test.)
A function \(f(x)\) is continuous on the interval \( (-\infty,\infty) \). The sign chart for \(f'(x)\) is shown below.
Show how to use the First-Derivative Test to find the \( x \) coordinates of all local extrema of \(f(x)\).
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see [Example 1] on page 9 of the Notes for the Video for Homework 56 .)
Instructor: Today we'll be discussing concepts from book Section 4.2, which is about 2nd Derivatives and Graphs.
The section begins with a definition of concavity and inflection point. In the videos for the course, this definition is found in the Video for H57. Here is the definition:
In our first Class Drill for today, you will practice drawing graphs with instructions that use the terminology of positive & negative, increasing & decreasing, and , concave up & down.
Draw four examples (four separate graphs) of functions \(f(x)\) on the domain \(1 \lt x \lt 5\)
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see Notes from the Video for H57 .)
Instructor: The study of concavity of \( f(x) \) leads us to investigate the derivative of the derivative of \( f(x) \). This is what is called the second derivative of \( f(x) \), and denoted \(f''(x)\). In the videos for the course, this definition is found in the Video for H57. Here is the definition:
Immediately following the above definition Video for H57, Barsamian presents this important correspondence:
Here is another short Class Drill that will give you practice using the correspondence just introduced.
Draw four examples (four separate graphs) of functions \(f(x)\) on the domain \(1 \lt x \lt 5\)
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see Notes from the Video for H57 .)
Instructor: Finding \(f''(x)\) can be very easy, but sometimes it is tricky. Here is a Class Drill where you will be asked to find \(f''(x)\).
Instructor: Show the solution to the Class Drill.
Instructor: In the Homework for Section 4.2, you do problems involving graphing. A Graphing Strategy was presented in the book and in the Video for H60. (See page 7 of the Notes for the Video for H60). Here is that Graphing Strategy:
Step 1: Analyze \(f(x)\). Find the domain and the axis intercepts. The \(x\) intercepts are the solutions of the equation \(f(x)=0\), and the \(y\) intercept is the value of \(f(0)\).
Step 2: Analyze \(f'(x)\). Find the partition numbers for \(f'\) and the critical numbers of \(f\). Construct a sign chart for \(f'\), determine the intervals on which \(f\) is increasing and decreasing, and find the local maxima and minima of \(f\).
Step 3: Analyze \(f''(x)\). Find the partition numbers for \(f''\). Construct a sign chart for \(f''\), determine the intervals on which \(f\) is concave up and concave down, and find the inflection points of \(f\).
Step 4: Sketch the graph of \(f(x)\). Locate axis intercepts, local maxima and minima, and inflection points. Sketch in what you know from steps 1-3. Plot additional points as needed to complete the sketch.
Problems involving using the Graphing Strategy can be quite long, because each of the four steps in the strategy is long. But there are some problems where you are given some information about \(f(x)\) and \(f'(x)\) and \(f''(x)\), and then asked to sketch a graph of \(f(x)\). Realize that such problems are still about the Graphing Strategy; they have simply been shortened by giving you a bunch of the information that you would have had to determine for yourself in Step 1, Step 2, and Step 3. Here is an example of that type.
Instructor do this [Example]: Sketch the graph of a function \( f(x) \) that has the properties listed below. Make your graph large and neat, and label all important points (axis intercepts, maxs and mins, inflection points) with their \( (x,y) \) coordinates. Draw horizontal tangent lines where needed, and label them with \( m=0 \).
Instructor: Today we'll be discussing concepts from book Section 4.5, which is about Absolute Extrema.
It is important to understand the distinction between Absolute Extrema (from Section 4.5 of the book) and Local Extrema (first introduced in Section 4.1). The general idea is that a local max is the greatest \(y\) value nearby, while an absolute max is the greatest \(y\) value on the whole domain.
Instructor: Write the definitions for local max and absolute max on the board. (Or refer to pages 3,4 in the Notes from the Video for H61).
Realize that the locations of and absolute extrema often don't match, and in many situations one or the other type of extremum may not even exist at all. (Show [Example 1] on page 5 of the Notes from the Video for H61 involving a function \(f(x)\) given by a graph.)
As seen in the example that was just projected, a particular function \(f(x)\) may not have an absolute min or absolute max on a particular domain. But there is a situation in which some absolute extrema are guaranteed to occur, and to occur only at certain possible locations.
Instructor: Write out Theorem 1: Extreme Value Theorem and Theorem 2: Locating Absolute Extrema on the board. (or refer to page 5 of the Notes from the Video for H62.)
The two theorems just presented are the basis for what is called the .
Instructor: In the case of a function \(f(x)\) that is continuous on a closed interval \([a,b]\), the absolute extrema of \(f(x)\) on the interval \([a,b]\) are found using a procedure called the Closed Interval Method.
Instructor: Write the steps for the Procedure for Finding Absolute Extrema on a Closed Interval on the board. (or refer to page 6 of the Notes from the Video for H62).
In our first Class Drill for today, you will do a basic example involving this new method.
Show how to use the Closed Interval Method to find the absolute extrema of \(f(x)=2x^3-3x^2-12x+7\) on the interval \( [-2,4]\).
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see pages 7 - 8 of the Notes from the Video for H62 .)
For Class Discussion
To find the absolute extrema of \(f(x)=x^3-3x+4\) on the interval \( [-2,3]\), one starts by finding \( f'(x)=3x^2-12x+9=3(x+1)(x-1) \), which has partition numbers \(x=-1\) and \(x=1\).
Question For the Class: Why isn't \(x=3\) also a partition number for \(f'(x)\)? It looks to be a very important number in the factorization of \(f'(x)\). And why isn't \(x=0\) a partition number? Explain why neither \(x=3\) nor \(x=0\) is a partition number.
Answer: Remember that a partition number for \(f'(x)\) is defined to be an \(x\) value such that \(f'(x)\) is undefined or \(f'(x)=0\). Since \(f'(x)\) is a polynomial, we know that there are no \(x\) values that will cause \(f'(x)\) to be undefined. Therefore, the only partition numbers for \(f'(x)\) will be the \(x\) values such that \(f'(x)=0\).
It is easy to confirm that \(x=-1\) and \(x=1\) are partition number for \(f'(x)\) by simply substituting \(x=-1\) and \(x=1\) into \(f'(x)\) and computing the result. The computation is easiest if we use the factored form, \( f'(x)=3(x+1)(x-1) \).
Now observe what happens if we try substituting \(x=0\) and \(x=3\) into \(f'(x)\) and computing the result. Again, the computation is easiest if we use the factored form of \(f'(x)\).
It is important to realize that absolute extrema do not always happen at \(x\) values that are integers. In our second Class Drill for today, you will again use the Closed Interval Method., but this time, you'll see an absolute extremum occur at a non-integer \(x\) value.
Show how to use the Closed Interval Method to find the absolute extrema of \(f(x)=x^4-4x^2 +5\) on the interval \( [-1,2]\).
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see pages 12 - 13 of the Notes from the Video for H62 .)
Quiz Q6 during the last part of the Fri Jul 12 class meeting
No Books, no Notes, no Calculators, no Phones, no Smart Watches
The quiz material is taken from the material covered in book Sections 3.4, 4.1, and 4.2. See the List of Homework Assignments for links to the corresponding Instructional Videos.
Sections, Content, Homework, and Videos:
Instructor: On Friday, we discussed Absolute Maxima and Absolute Minima. We also discussed the fact that for a function \(f(x)\) that is continuous on a closed interval \([a,b]\), the absolute extrema of \(f(x)\) on the interval \([a,b]\), it is guaranteed that the function will have both an absolute max and an absolute min on that interval. On Friday, we discussed that in this case, the absolute extrema are found using a procedure called the Closed Interval Method.
Today, we will discuss the case of a function \(f(x)\) that is continuous on a domain that is not a closed interval. In this case, the function is not guaranteed to have any absolute extrema at all. Often, it is helpful to determine whether there will be an absolute max or absolute min before finding them precisely. In the following short Class Drill, you'll have to think about how that might be done.
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see [Example 1] on page 7 of the Notes from the Video for H63 .)
Instructor: For some functions that are not a familiar form, on domains that are not closed intervals, it is not possible to figure out whether there will be any absolute extrema without doing any calculations.
For example, suppose we want to find out if the function $$f(x)=4x+\frac{128}{x^2}$$ will have any extrema on the interval \( (0,\infty) \). Observe that \(f(x)\) is continuous on the interval \( (0,\infty) \), but the interval is not a closed interval. We have seen that in situations where the domain is not a closed interval, a function \(f(x)\) might not even have an absolute min or absolute max. We'll discuss this example now.
Instructor Do this Example: Find the absolute max and absolute min, if they exist, for the function $$f(x)=4x+\frac{128}{x^2}$$ on the interval \( (0,\infty) \). As part of the solution, introduce the Second Derivative Test. (For reference, see [Example 2] on page 14 of the Notes from the Video for H63 .)
Instructor: For the rest of today's meeting, we'll start a discussion of Optimization, from Section 4.6 of the book. Although the topic sounds like something new, realize that Optimization problems are just Absolute Max/Min problems, but with some complications.
Today, we'll be discussing Single Variable Optimization Problems about Maximizing Revenue and Profit
In the Video for H64, Barsamian discusses
That means that of the possible complications listed above you will have to deal with #1,2,4, but not #3. Our discussion about Optimization today will be about problems of that sort.
[Example: Hoverboards] This is the continuation of an example that was started in the Jun 12 meeting (Day 13).
A company makes hoverboards, a very dangerous toy that kids would not ride if they had a lick of sense. The price demand equation is
$$x=6,000-30p$$where \(p\) is the selling price of a hoverboard, in dollars, and \(x\) is the number of hoverboards that will sell at that price.
In the Jun 12 meeting, you found in a Class Drill that the price function is $$p(x)= \left(-\frac{1}{30}\right)x+200$$ with domain $$ [0,6000] $$ You saw that the graph of the price function will be a line segment with endpoints at \((0,200)\) and \((6000,0)\).
You also found the Revenue function is $$R(x) = \left(-\frac{1}{30}\right)x^2 + 200x $$ with domain $$[0,6000]$$ You saw that the graph of the Revenue function will be a chunk of a parabola
In our first Class Drill for today, you will revisit this example, this time with the goal of maximizing Revenue
Use the revenue function \(R(x) = \left(-\frac{1}{30}\right)x^2 + 200x\) with domain \([0,6000]\) that was discussed above.
(a) If the goal is to maximize Revenue, what price should the company charge for the hoverboards, and how many hoverboards should be produced? Illustrate your solution with a graph of the Revenue function.
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see [Example 1] on page 8 of the Notes from the Video for H64. .)
In our second Class Drill for today, you will continue this example, this time with the goal of maximizing Profit
You will be continuing the example from the previous Class Drill, using the Revenue function \(R(x) = \left(-\frac{1}{30}\right)x^2 + 200x\) with domain \([0,6000]\) that was discussed above.
Suppose also that the Cost function is \(C(x) = 60,000 + 20x\)
(b) Find the Profit function, \(P(x)\).
(c) If the goal is to maximize Profit, what price should the company charge for the hoverboards, and how many hoverboards should be produced? Illustrate your solution with a graph of the Profit function.
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see [Example 1] on page 8 of the Notes from the Video for H64. .)
Instructor: On Monday, we began a discussion of Optimization Problems. Remember that Optimization problems are just Absolute Max/Min problems, but with some complications.
On Monday, we discussed Single Variable Optimization Problems about Maximizing Revenue and Profit
We'll start today's meeting by discussing another kind of problem of that sort.
Often, in problems about Revenue and Profit, the variable is the Demand, which is customarily denoted by the letter x. Sometimes, though, the Demand is not the most convenient variable. In those cases, it might be clearer to us a different letter, besides x, for the variable. The problems of this type can seem very strange at first: It is often not obvious what the variable should even be. But with practice, the problems can become familiar. Students will spend the rest of the class meeting working on a Class Drill that is a problem of this type. (The problem has wording similar to book Section 4.6 Example 6 and Exercises 4.6 # 25, 27, which are MyLab Homework H64 problems [2] and [3].)
Students: Work on the following Class Drill: When the Variable is Not the Demand
Instructor: Show the solution to the Class Drill that the students just worked on. (For reference, see [Example 2] on page 9 of the Notes from the Video for H64 .)
The Video for H65 (link to accompanying notes) discusses
In these problems, of the possible complications discussed earlier (complications that Optimization Problems may or may not have), you will have to deal with #3,4, but not #1,2. In this second part of our meeting for today, we'll see an example of that sort.
Instructor do this [Example]: (This example is similar to a problem in the Homework for Section 4.6)
Find positive numbers \(x,y\) such that
Observe that this problem does involve two variables, but it is not about some real world situation. Hence, we could call it a two variable abstract optimization problem.
(For reference, see [Example 1] on page 8 of the Notes from the Video for H65 .)
The Video for H66 (link to accompanying notes) discusses
In these problems, of the four possible complications listed earlier in the meeting outline, you will have to deal with all four! In our Class Drill. You will solve a problem of that sort in a Class Drill.
A farmer needs to build a fence to make a rectangular corral next to an adjacent pasture. He only needs to fence three sides, because the fourth side has already been fenced. He has 1200 feet of fencing. Find the dimensions of the pasture that will enclose the largest possible area.
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see [Example 1] on page 3 of the Notes from the Video for H66 .)
Instructor: Notice that the mathematical model that you arrived at in your Class Drill exactly matches the two variable abstract optimization problem that I solved in the preceeding Example.
Exam X2 lasts the full duration of the Fri Jul 19 class meeting
No Books, no Notes, no Calculators, no Phones, no Smart Watches
The exam material is taken from the material covered in Chapters 3 and 4. See the List of Homework Assignments for links to the corresponding Instructional Videos.
Sections, Content, Homework, and Videos:
Instructor: Today we'll be discussing concepts from book Section 5.1, which is about Antiderivatives and Indefinite Integrals.
We'll start with the definition of Antiderivative
Observe that to answer the question
the strategy is to
Instructor Example: Show how to use that strategy to answer these questions: $$\begin{eqnarray} \text{(a) Is } \ F(x) &=& \frac{x^3}{3} \ \text{ an antiderivative of } \ f(x) = x^2 \ \text{?} \\ \text{(b) Is } \ F(x) &=& \frac{(5x+7)^3}{3} \ \text{ an antiderivative of } \ f(x) = (5x+7)^2 \ \text{?} \end{eqnarray} $$
Instructor: You’ll work on more of these kinds of questions in the following Class Drill.
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see [Example 3] on page 4 of the Notes from the Video for H68 .)
Instructor: Questions (c) and (d) that you just worked on illustrate that a given function \( f(x) \) will have a whole family of antiderivatives that differ from each other by an additive constant. This is articulated as a Theorem about the Collection of Antiderivatives of a Function. (Instructor present the theorem and illustrate it by drawing the family of antiderivatives of \( f(x) = x^2 \).) (See pages 4-7 of the Notes from the Video for H69 for reference.)
Instructor: Discuss the distinction between Particular Antiderivative and General Antiderivative. (See pages 8-9 of the Notes from the Video for H69 for reference.)
Instructor: Introduce the Indefinite Integral of \( f(x) \) (See page 7 of the Notes from the Video for H70 for reference.)
Instructor: Present the Power Rule, the \(\frac{1}{x}\) Rule, the \(e^{(x)}\) Rule, the \( \ln(x)\) Rule, and the Sum and Constant Multiple Rule, (See page 6 of the Notes from the Video for H71 for reference.) (Put these on the board in a place where they can stay up for the rest of the meeting.)
Instructor: Show the details of the calculation of the following indefinite integral $$ \int 7\sqrt x dx$$
Instructor: You’ll use the Indefinite Integral Rules that I just wrote down when you work in the following Class Drill.
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see [Example 1] on page 22 of the Notes from the Video for H70 .)
Instructor: It is important to pay attention to when the Power Rule for Indefinite Integrals can be used and when it cannot be used. For example, we already know that
$$\int \frac{1}{x} dx = \ln(|x|) + C$$Here are three common incorrect indefinite integrals of \(\frac{1}{x}\). Observe that each of them involves using the Power Rule, which is the wrong rule!
$$\begin{eqnarray} \text{Incorrect integral #1: } \ &\int& \frac{1}{x} dx &=& \int x^{-1} dx = \frac{x^{(-1)+1}}{(-1)+1}+C = \frac{x^0}{0}+C = \frac{1}{0}+C = \text{undefined} \\ \text{Incorrect integral #2: } \ &\int& \frac{1}{x} dx &=& \int x^{-1} dx = \frac{x^{(-1)+1}}{(-1)+1} = \frac{x^0}{0} = \frac{1}{0}= 0 \\ \text{Incorrect integral #3: } \ &\int& \frac{1}{x} dx &=& \int x^{-1} dx = \frac{x^{(-1)+1}}{(-1)+1}+C = \frac{x^0}{0}+C = \frac{1}{0}+C = 0+C=C \\ \end{eqnarray} $$Instructor: It is also important to remember that finding Indefinite Integral is not the same as finding a Derivative.
For example, we know that $$\frac{d}{dx}\ln(x)=\frac{1}{x}$$ while $$ \int \ln(x) dx = x\ln(x)-x+C. $$ And we know that $$\frac{d}{dx}1=0$$ while $$ \int 1 dx = x+C. $$
Instructor: The definition of Antiderivative was first introduced in the Video for H68 and is reviewed at the start of the Video for H71 (Project page 2 of the Notes from the Video for H71 .)
Recall that for a given function \(f(x)\), there will be a collection of antiderivatives. This collection is called the General Antiderivative of \( f(x) \) and is also called the Indefinite Integral of \( f(x) \). And remember the relationship between the indefinite integral and \( f(x) \) (page ahead to pages 4 and 5 of the notes for the Video for H71.)
In your reading of the book or watching of the videos, you learn a collection of Indefinite Integral Rules.
The Power Rule for Indefinite Integrals:
$$ \int x^n dx = \frac{x^{n+1}}{n+1}+C \ \ when \ \ n \neq -1 $$The \( \frac{1}{x} \) Rule for Indefinite Integrals:
$$ \int \frac{1}{x} dx = \ln{(|x|)}+C $$The \( e^{(x)} \) Rule for Indefinite Integrals:
$$ \int e^{(x)} dx = e^{(x)}+C $$The \( \ln{(x)} \) Rule for Indefinite Integrals:
$$ \int \ln{(x)} dx = x\ln{(x)}-x+C $$The Constant Multiple Rule for Indefinite Integrals:
$$ \int af(x) dx = a\int f(x) dx $$The Sum Rule for Indefinite Integrals:
$$ \int f(x)\pm g(x) dx = \int f(x) dx \pm \int g(x) dx$$The Sum and Constant Multiple Rule for Indefinite Integrals:
$$ \int af(x)\pm bg(x) dx = a\int f(x) dx \pm b\int g(x) dx$$Instructor: Look at the list of Indefinite Integral Rules. Notice that there is no Quotient Rule in the list. And observe that there is only one Indefinite Integral Rule shown in the table where the integrand is a quotient.
$$ \int \frac{1}{x} dx = \ln(|x|) + C $$Integrals where the integrand is a more general quotient have to be treated carefully. For some integrals where the integrand is a general quotient, it is possible to first rewrite the integrand in power function form, and then find the integral using the sum and constant multiple rule and the power rule.
Instructor do this Example: Consider the indefinite integral $$ \int \frac{4}{\sqrt[3]{x}} + \frac{5}{x^4} dx $$
Instructor: Pose this Question to the Class Three students were assigned the problem of finding an indefinite integral. Here are their solutions: $$\begin{eqnarray} \text{Student 1 wrote: } \ \int \frac{3}{5x^2} dx &=& \frac{3}{5\cdot \frac{x^3}{3}} + C = \frac{9}{5x^3} + C \\ \text{Student 2 wrote: } \ \int \frac{3}{5x^2} dx &=& \int 3\cdot 5x^{-2} dx = \frac{3 \cdot 5x^{-1}}{-1} + C = -\frac{3}{5x} + C \\ \text{Student 3 wrote: } \ \int \frac{3}{5x^2} dx &=& \int \frac{3}{5} \cdot x^{-2} dx = \frac{3}{5} \cdot \frac{x^{-1}}{-1} + C = -\frac{3}{5x} + C \end{eqnarray}$$ Which student(s) wrote a correct solution to the problem? Explain.
It is important to realize that some fractions in integrands need to be left as fractions. For example, if the integrand contains a \( \frac{1}{x} \), then that term should be left alone, not converted into the power function form \( x^{-1} \). The reason is that the indefinite integral $$ \int x^{-1} dx $$ cannot be found using the Power Rule, while the indefinite integral $$ \int \frac{1}{x} dx $$ can be found using the \( \frac{1}{x} \) Rule. $$\int \frac{1}{x} dx = \ln(|x|) + C$$
In the following Class Drill, you will need to rewrite the integrand involving a quotient so that part of it is converted to power function form while part of the integrand is left in \(\frac{1}{x}\) form
Consider the indefinite integral $$ \int \frac{1+x^3}{x} dx $$
Instructor: Show the solution to the Class Drill that the class just worked on. (For reference, see [Example 1](F) on page 12 of the Notes from the Video for H71 .)
Instructor: A type of problem that you will encounter in your Homework for Section 5.1 involves finding a particular antiderivative satisfying an extra condition.
The strategy for finding a particular antiderivative satisfying an extra condition is to
Instructor do this Example: Find the particular antiderivative of the derivative $$ \frac{df}{dx} = 3e^{(x)} - 4 $$ that satisfies \( f(0) = 8 \). (See [Example 3] on page 13 of the Notes from the Video for H72 for reference.)
Instructor: Note that \(x\) is not always the letter used as the variable. And \(f\) is not always the letter used as the name of the function. In particular, it is common to use the variable \(t\), indicating time. And in Engineering and Physics, it is common to have a function called \(x(t)\) that gives the position, at time \(t\), of an object moving in one dimension. Using this kind of notation, the example problem that I just solved would be stated as follows:
Find the particular antiderivative of the derivative $$ \frac{dx}{dt} = 3e^{(t)} - 4 $$ that satisfies \( x(0) = 8 \). Show all steps clearly.
This wording of the problem is the same as the wording used on a related problem in your Mylab Homework for Section 5.1.
Realize that the solution would be exactly the same as the solution presented in the previous example, but with the variable changed from \(x\) to \(t\) and the function name changed from \(f\) to \(x\)
Instructor: Today, we'll be discussing the method of Integration by Substitution. This method is used to find an integral in some situations where the integrand involves a nested function, also known as a composition of functions. Different books present this method in different ways. In the videos for our course, a 5-Step procedure is presented.
Step 1: Identify the inner function and call it \(u\). Write the equation \(inner(x)=u\) to introduce the single letter \(u\) to represent the inner function. Circle the equation.
Step 2: Build the equation \(dx=\frac{1}{u'}du\). To do this, first find \(\frac{du}{dx}\), then use it to build equation \(dx=\frac{1}{u'}du\). Circle the equation.
Step 3: Substitute, Cancel, Simplify. In steps (1) and (2) you have two circled equations. Substitute these into the integrand of your indefinite integral. Cancel as much as possible and simplify by using the Constant Multiple Rule. The result should be a new basic integral involving just the variable \(u\).
Step 4: Integrate. Find the new indefinite integral by using the indefinite integral rules. The result should be a function involving just the variable \(u\) (with constant of integration \(+C\) ).
Step 5 Substitute Back. Substitute \(u=inner(x)\) into your function from Step (4). The result will be a new function of just the variable \(x\). (Be sure to include the constant of integration \(+C\) ) in your result.) This is the \(F(x)\) that we seek.
The first step of the Substitution Method presented in the Video is to identify the inner function and call it \(u\). Once \(u\) has been identified, everything else in the procedure unfolds without any choices to be made.
Question #1 for the Class: For the integral $$ \int 2x\left(x^2+4\right)^7dx $$ What should you choose as the \(u\)?
Instructor: As mentioned in the Video for H74, identifying \(u\) can be straightforward when the inner function is in parentheses and nothing else in the integrand is in parentheses. In some integrals, however, the choice of \(u\) is not so obvious. Furthermore, in some of the problems in our book and in MyLab, the choice of \(u\) is made harder by the weird and misleading typesetting used by the publisher. The publisher sometimes puts parentheses where they are not needed and omits them in places where it would be helpful to have them.
Question #2 for the Class: For the integral $$ \int e^{5x}(5)dx $$ What should you choose as the \(u\)?
Question #3 for the Class: For the integral $$ \int \sqrt{1+4x^2}(8x)dx $$ What should you choose as the \(u\)?
Question #4 for the Class: For the integral $$ \int \frac{1}{4+2x^4}\left(8x^3\right)dx $$ What should you choose as the \(u\)?
Question #5 for the Class: For the integral $$ \int \frac{1}{9x+5}dx $$ What should you choose as the \(u\)?
Instructor: As mentioned earlier, if you follow the procedure for the Substitution Method that is presented above, once you identify \(u\), there are no choices to be made in the procedure. (And note that the identification of \(u\) is not really a choice. Either \(u\) works, or it doesn't.) But some substitution problems are easier than others because of the way that all of the constants cancel nicely in the substitution step.
For example, In the next two class drill, you will finish the problems started as Questions #4 and #5 for the class, above.
Instructor: Divide the class into two clubs: the Jets and the Sharks. Within each club, have students work on the Substitution Problem for their Club. Remind them to show all steps clearly and use correct notation.
$$\begin{eqnarray} \text{Jets work in pairs to find } \ &\int& \frac{8x^3}{4+2x^4}dx \\ \\ \text{Sharks work in pairs to find } \ &\int& \frac{1}{9x+5}dx \end{eqnarray}$$Instructor: Show the solutions to the problems that the Jets and the Sharks just worked on. (For reference, see the [Example 1D] in the Notes from the Video for H74 .)
Instructor: Notice that the integral that the Jets had to find looked harder than the integral that the Sharks had to find. But all the messy stuff cancelled in Step 3 of the Jets' solution, while in Step 3 of the Sharks' solution, there was a leftover constant, which made that problem a little harder.
In the Video for H74 and the Video for H75 there is extensive discussion of more types of integrals involving the Substitution Method. You'll work on a couple more types in the following Class Drill.
Instructor: Have students work in pairs for 20 minutes on Two Class Drills on Indefinite Integrals (Sections 5.1 and 5.2) After 20 minutes, discuss the solutions.
Sections, Content, Homework, and Videos:
Instructor: Today we'll be discussing the the area between the graph of a function \( f(x) \) and the \(x\) axis from \(x=a\) to \(x=b\). A picture of this can be found on page 2 of the Notes from the Video for H76.
As discussed in the video, there are two kinds of area that we will be studying
When a region is made up of basic geometric shapes, we can compute both kinds of areas using formulas from geometry.
Instructor: You will now work on a problem about computing both kinds of areas using formulas from geometry in a Class Drill.
Instructor: Hand out the multi-part Class Drills on Area and Definite Integrals.
Students: work on Class Drill: Finding Unsigned and Signed Areas Using Geometry. (Just the first one of the four class drills on the handout.)
Instructor: Show the solutions to the Class Drill that the class just worked on. (For reference, see [Example 1] on page 3 of the Notes from the Video for H76. You might want to print out the drill ahead of Monday's meeting, so that you can practice showing how the solution goes.
Instructor: (Project page 5 in the Notes from the Video for H76) But when the region between the graph of \(f(x)\) and the \(x\) axis from \(x=a\) to \(x=b\) is not made up of basic geometric shapes, the definition of what its area even means, and the computation of its value, presents a very sophisticated problem, called the Area Problem. The Area Problem could be articulated in the following Two Questions about Area:
The Area Problem (Two Questions about Area)
The solution of the Area Problem is a long, detailed process that you should learn about by reading the book and/or watching the Video for H76. In our meeting, we will only discuss some aspects of what is presented in detail in the book and in the video.
The approach to solving the Area Problem for a curvy region is to first consider an approximation of the region using a simpler region made up of basic geometric shapes. One can find the area of the simpler region using geometry.
Instructor: We will now work together on a problem about Estimating the Area Under a Graph in Class Drill.
Instructor: Using the Document Camera, lead the students in the solution of Class Drill: Estimating the Area Under a Graph Using Riemann Sums (Just the second of the four class drills on the handout.).
(For reference, see the Video for H76 and read pages 7 - 22 in the Notes from the Video for H76. The video would have benefited from a simple, visual example presented before the difficult analytical material. (Mark B says Sorry!!) The Class Drill is that kind of simple, visual example.)
Instructor: On page 7 of the Notes from the Video for H76, a Quest begins:
Quest: Find the value of the signed area between the graph of $$f(x)=5+\frac{x^2}{10}$$ and the \(x\) axis from \(x=2\) to \(x=12\).
On page 9 of the notes, you can see the region in question shaded in Blue and sandwiched in between a Green Region and a Red Region. The Blue Region is curvy, and we don't know how to compute its area. But the Green and Red Regions are made up of simple geometric shapes (rectangles) whose area we can compute exactly. We can use those Green and Red areas to get lower and upper bounds on the area of the Blue region. (Note that the computations use the formula for \(f(x)\) to get the \(y\) values on the graph. This is in contrast to what the students did in their last class drill, where they just got the \(y\) values from the graph.)
The area of the Green Region is called the Left Sum with 5 Subintervals, denoted \(L_5\); the area of the Red Region is called the Right Sum with 5 Subintervals, denoted \(R_5\). The result of the example, presented on page 22 of the Notes, is the following estimate of the area of the Blue Region.
$$95=L_5 \lt \ Blue \ Area \lt R_5 = 122$$In [Example 4] on page 26 of the video, better lower and upper bounds for the unknown Blue area are found by finding Left sums \(L_n\) and Right Sums \(R_n\) with larger and larger values of \(n\). Two trends are observed:
It turns out that the two trends observed in [Example 4] of the video will always be observed. On page 31 of the Notes, the following Big Fact is presented:
The Big Fact: It is a fact from more advanced math that for a function \(f(x)\) that is continuous on a closed interval \([a,b]\), the values of \(L_n\) and \(R_n\) always approach some common number as \(n\rightarrow\infty\). That is, \(\lim_{n\rightarrow\infty}L_n\) and \(\lim_{n\rightarrow\infty}R_n\) both exist and \(\lim_{n\rightarrow\infty}L_n = \lim_{n\rightarrow\infty}R_n\).
The Big Fact gives us a way to define the signed area of the region between the graph of a general curvy function \(f(x)\) and the \(x\) axis on a closed interval \([a,b]\), and also compute its value. We can just define the signed area to be the number that is the limit of the Riemann Sums. Notice that this answers the Two Questions about Area that make up The Area Problem.
Because the definition is so important, it gets a name (and a symbol): the Definite Integral. (See page 33 of the Notes from the Video and discuss the Definition of the Definite Integral and Signed Area.)
$$ SA \overset{\text{def}}{=} \ \text{Definite Integral of} \ f(x) \ \text{from} \ x=a \ \text{to} \ x=b \ \overset{\text{def}}{=} \int_{x=a}^{x=b} f(x)dx \overset{\text{def}}{=} \lim_{n \rightarrow \infty} L_n = \lim_{n \rightarrow \infty} R_n $$Instructor: (only if there is enough time) Have Students work on this Class Drill.
Students: Work on Class Drill: Using Properties of the Definite Integral. (Just the third of the four class drills on the handout.)
Instructor: Show the solutions to the Class Drill that the class just worked on.
Instructor: (only if there is enough time) In the Class Drill just done, the graph of a function \(f(x)\) was given, along with the values of the unsigned areas of certain regions between the graph and the \(x\) axis. Those given values of the unsigned areas were used to give values for certain definite integrals.
In the last Class Drill for today, the graph of a function \(f(x)\) is given, but there are no given unsigned areas. Instead, you will have to figure out the areas of the regions using geometry.
Instructor: (if there is enough time) Have Students work on this Class Drill.
Students: Work on Class Drill: Definite Integrals for a Simple Graph . (Just the fourth of the four class drills on the handout.)
Instructor: Show the solutions to the Class Drill that the class just worked on.
The Area Problem
Instructor: Recall that on Monday, we discussed the Area Problem, or "Two Questions about Area":
After much discussion (See the Notes from the Video for H76), we arrived at a definition the Signed Area that involved Riemann Sums. The resulting definition fo the Signed Area was given a new name: The Definite Integral.
$$ SA \overset{\text{def}}{=} \ \text{Definite Integral of} \ f(x) \ \text{from} \ x=a \ \text{to} \ x=b \ \overset{\text{def}}{=} \int_{x=a}^{x=b} f(x)dx \overset{\text{def}}{=} \lim_{n \rightarrow \infty} L_n = \lim_{n \rightarrow \infty} R_n $$Is There An Easier Way?
Video H76 ended with some discussion about the difficulty of the computations involved in finding the value of a definite integral using the definition of the integral as a limit of Riemann Sums. A question was posed:
The answer to that question is yes; the easier way is to use what is called the Fundamental Theorem of Calculus.
The Fundamental Theorem of Calculus expresses the relationship between definite integrals and antiderivatives. The Theorem is presented on pages 7 - 8 of the Notes from the Video for H78. The notation in Book Section 5.5 and in the Video Notes on page 8 is standard notation for the theorem, but it is perhaps hard to understand and hard to remember. In the video, Barsamian gives another presentation of the theorem, using change in \(F\) notation.
Instructor: Introduce change in \(F\) notation and give an example of its use. (For reference, see page 17 in the Notes from the Video for H78.)
(the relationship between definite integrals and antiderivatives)
If \(f(x)\) is continuous on the interval \([a,b]\), then
$$\int_a^bf(x)dx\underset{\text{FTC}}{=}\left. \left(\int f(x)dx\right)\right\vert_a^b$$This notation may help you better understand the statement of the theorem, and better remember how to use the theorem.
Instructor Do this Example (Using the notation as described above and introduced in the Video for H78). Show why
$$ \int_{2}^{12} 5+\frac{x^2}{10} \ dx = \frac{322}{3} = 107.\overline{333}$$This result is interesting because it is an exact result, not particularly hard to obtain, and it confirms the estimate that was obtained in Video H76. That is:
Instructor: In the MyLab system, problems about finding the value of a definite integral using the Fundamental Theorem of Calculus are not very well written. They simply ask you to type in the value of the definite integral. They don't ask you to show any of the steps that lead to that value. This style of problem is easy for the publisher to produce, but it does not test your understanding of the problem. And, if you don't understand the problem, those online questions that just ask you to enter the final answer will not help you gain an understanding.
Focusing on the steps that lead to the answer is the best way to improve your understanding of the Fundamental Theorem. For that reason, today's Class Drills and Presentations are all about showing the steps that lead to an answer. In fact, the answers will be given to you. Your job will be to show the steps.
Instructor: Have students work on the following Drill problem #1: A definite integral is shown below, along with the correct answer. Show how the answer is obtained. (Show the steps.)
$$\int_{3}^{5}4x^3+5 \ dx = 554$$Instructor: Show the solution of Drill problem #1: (For reference, see [Example 4] on page 20 of the Notes from the Video for H78.)
Instructor: Have students work on the following Drill problem #2: A definite integral is shown below, along with the correct answer. Show how the answer is obtained. (Show the steps.)
$$ \int_{3}^{4}\frac{2}{x^2} \ dx = \frac{1}{6}$$Instructor: Show the solution of Drill problem #2: (For reference, see [Example 5] on page 22 of the Notes from the Video for H78.)
Instructor: Have students work on the following Drill problem #3: A definite integral is shown below, along with the correct answer. Show how the answer is obtained. (Show the steps.)
$$ \int_{0}^{1}6\sqrt[6]{x} \ dx = \frac{36}{7} $$Instructor: Show the solution of Drill problem #3: (For reference, see [Example 7] on page 24 of the Notes from the Video for H78.)
Instructor: Have students work on the following Drill problem #4: A definite integral is shown below, along with the correct answer. Show how the answer is obtained. (Show the steps.)
$$ \int_{6}^{3}2x+5 \ dx = -42$$Instructor: Show the solution of Drill problem #4: (For reference, see [Example 9] on page 26 of the Notes from the Video for H78.)
Instructor: Have students work on the following Drill problem #5: A definite integral is shown below, along with the correct answer. Show how the answer is obtained. (Show the steps.)
$$ \int_{7}^{28}\frac{3}{x} \ dx = 3\ln{(4)}$$Instructor: Show the solution of Drill problem #5: (For reference, see [Example 6] on page 23 of the Notes from the Video for H78.)
Instructor: For Drill problem #5 just presented, Wolfram Alpha says that the answer is $$ \int_{7}^{28}\frac{3}{x} \ dx = \log{(64)}$$ But if you type \( \log(64) \) into a MyLab answer box for this problem, it will be marked incorrect!
Questions for the Class:
Answer: First, note that the correct answer can be presented in different forms: $$ \int_{7}^{28}\frac{3}{x} \ dx = 3\ln{(4)} = \ln{(4^3)} = \ln{(64)}$$ Indeed, if you enter \(3\ln{(4)}\) or \(\ln{(4^3)}\) or \(\ln{(64)}\) into a MyLab answer box for this problem, it will be marked correct!
Next note that
Because of this, when Wolfram Alpha gives an answer \( \log(64) \), it means the natural logarithm of \(64\).
But if you enter \( \log(64) \) into a MyLab answer box for this problem, MyLab will interpret your answer as the base \(10\) logarithm of \(64\). That answer is incorrect.
This illustrates that using handheld or online calculators makes some computations easier, but also requires that you be aware of complications that may arise.
Instructor: Have students work on the following Drill problem #6: A definite integral is shown below, along with the correct answer. Show how the answer is obtained. (Show the steps.)
$$ \int_{0}^{4}e^{(2x)} \ dx = \frac{e^8-1}{2} \approx 1489.979$$Instructor: Show the solution of Drill problem #6: (For reference, see [Example 8] on page 25 of the Notes from the Video for H78.)
Instructor: Sometimes, computations of Definite Integrals will involve associated Indefinite Integrals that must be found using the Method of Substitution.
Instructor: Have students work on the following Drill problem #7: A definite integral is shown below, along with the correct answer. Show how the answer is obtained. (Show the steps.)
$$ \int_{0}^{1}42x\left(x^2-1\right)^{6} \ dx = 3$$Instructor: Show the solution of Drill problem #7: (For reference, see [Example 1] on page 4 of the Notes from the Video for H79.)
Instructor: Our first topic for today is Total Change Problems.
We begin by reviewing an old concept and introducing a new one.
The Old Concept: A very important concept for the second month of the course was the equality of three quantities related to slope:
The New Concept: An important concept in the final month of the course is the equality of three quantities related to area:
For now, we will discuss the equality of the first and third items on the list above. Later in this meeting, we will discuss the second item on the list.
In Section 5.5, on Homework H80 Total Change Problems, you are asked to find the total change in \(F(x)\) from \(x=a\) to \(x=b\) when the the derivative \(F'(x)\) is given. The point of those exercises is that you had to make the connection that the change in \(F(x)\) (the first item on the list above) is found by integrating \(F'(x)\) (the third item on the list above).
To understand why that is the approach, it is worth reviewing the different forms of the Fundamental Theorem of Calculus that Barsamian discusses on pages 3 - 5 of the Notes from the Video for H80 . Barsamian concludes the discussion on page 5 by presenting a green box describing Total Change Problems.
Our first Class Drill will be an example of a Total Change Problem.
A company manufactures electric scooters, a very dangerous gadget that people would not ride if they had a lick of sense. The Marginal Cost is $$C'(x)=400-\frac{x}{3}\text{ for }0\leq x\leq 900$$ where the variable \(x\) represents the number of scooters made per month (the quantity) and \(C'(x)\) is in dollars.
Find the increase in cost going from a production level of 600 scooters per month to 630 scooters per month. Show all details of the calculation clearly.
Instructor: Show the solution of the Class Drill. (For reference, see [Example 1] on page 6 of the Notes from the Video for H80 .)
Instructor: Next, we'll discuss the Average Value of a Function Over an Interval .
In the English language, the word average has a variety of meanings. But in Math & Science, the word average gets assigned certain precise meanings in different situations. One use of the word average is in the phrase Average Value of a Function Over an Interval. On pages 4 - 5 of the Notes from the Video for H81 , Barsamian poses a geometric question, and then answers the question. The answer to the question is presented in an official definition of the Average Value of a Function Over an Interval.
Our next Class Drill will be an example of computing the The Average Value of a Function over an Interval.
A drug is administered to a patient by a pill. The drug concentration in the bloodstream is described by the function $$C(t)=\frac{2t}{t^2+4}\text{ for }0\leq t \leq 12$$ where \(t\) is the time in hours after the pill is taken and \(C(t)\) is the drug concentration in the bloodstream (in micrograms/liter) at time \(t\).
Find the average drug concentration in the bloodstream over the first \(2\) hours. Give an exact answer and a decimal approximation. Show all details of the calculation clearly.
Instructor: Show the solution of the Class Drill. (For reference, see [Example 3](a) on pages 12-13 of the Notes from the Video for H81.)
Sections, Content, Homework, and Videos:
Instructor: Today, we'll begin discussing Area Between Curves (Concepts from Section 6.1).
In Chapter 5, we discussed the signed area between the graph of a function \(f(x)\) and the \(x\) axis, and we learned how to compute the value of the signed area using the definite integral.
It is important to note that the term Area Between Curves, as used in Chapter 6, refers to an unsigned area. We will eventually find the value of the unsigned area using a calculation involving definite integrals, but we must first be careful to set up the correct integral calculation. The process of setting up the correct integral calculation is discussed on pages 4 and 5 of the Notes from the Video for H82 . As explained there, the key is to scrutinize the graphs of the curves, and determine the simple regions.
In today's first Class Drill you'll work on setting up a definite integral to compute the area between two curves.
Instructor: Show the solution of the Class Drill that the class just worked on. (For reference, see Book Exercise 6.1#37, which is MyLab H83 problem [1], and [Example 1] on page 4 of the Notes from the Video for H83 .)
Instructor: In the Class Drill just finished, the graphs of the functions \(f(x)\) and \(g(x)\) were given, so the setting up of the correct definite integral calculation amounted to simply identifying the endpoints of the simple regions, then identifying the top and bottom functions for each region, and finally, setting up the definite integrals.
In practice, however, one is only given formulas for the functions \(f(x)\) and \(g(x)\), not their graphs. The problem of finding the area between the curves is then made significantly harder because one must first graph the functions \(f(x)\) and \(g(x)\). Then one must use the graphs of the curves to determine the simple regions and set up the correct definite integral calculation. Then, one must find the value of the definite integral calculation. These are difficult problems, as hard as anything in MATH 1350.
You will work on problems of this type in two Class Drills.
Instructor: Show the solution of the Class Drill that the class just worked on. (For reference, see [Example 2] on page 5 of the Notes from the Video for H83 and [Example 4] on page 9 of the Notes from the Video for H83 .)
Set up a definite integral to find the area bounded by the graphs of the equations \(y=e^x\) and \(y=-\frac{1}{x}\) over the interval \(1 \leq x \leq 3\). Then, find the value of the integral. Give an exact, simplified answer. Then, give a decimal approximation rounded to 3 decimal places
Instructor: Show the solution of the Class Drill that the class just worked on. (For reference, see [Example 3] on page 7 of the Notes from the Video for H83. .)
If there is time remaining: Instructor do this [Example]:
Set up a definite integral to find the area bounded by the graphs of the equations \(y=27\sqrt{x}\) and \(y=x^2\). Then, find the value of the definite integral. Give an exact, simplified answer. Then give a decimal approximation rounded to 3 decimal places.
Instructor: An important concept in the final month of the course is the equality of three quantities related to area:
On Homework H80 Total Change Problems, you are asked to find the total change in \(F(x)\) from \(x=a\) to \(x=b\) when the the derivative \(F'(x)\) is given. The point of those exercises is that you had to make the connection that the change in \(F(x)\) (the first item on the list above) is found by integrating \(F'(x)\) (the third item on the list above).
In Section 6.1, on Homework H84 Total Change Problems as Area Problems, you are asked to compute areas between graphs of \(F'(t)\) and the \(t\) axis over a time interval \(t=a\) to \(t=b\), and then to interpret the result. The point of these exercises is that you must first make the connection that the area (the second item on the list above) is computed by integrating \(F'(t)\) (the third item on the list above), and then make the connection that what that area represents is the change in \(F(t)\) from \(t=a\) to \(t=b\) (the first item on the list above). You'll work in pairs on a Class Drill of this sort.
An online group has formed consisting of people who have been injured in electric scooter accidents. In its early months of existence, the group is growing at a rate $$N'(t) = 1000e^{0.5t} \ \ users \ \ per \ \ month$$
Student #15 Presentation CP3: Show the solution of the Class Drill that the class just worked on. To prepare for this presentation, study
Instructor: The degree of income inequality in the United States is a common subject in conversation and in the news. There is a quantitative measure of income inequality that is based on measuring the area between curves. The quantitative measure is called the Gini Index.
The Gini Index is computed using a definite integral involving a function called a Lorenz Curve. In order to understand the Gini Index, we must first learn about that curve. The curve is introduced on pages 4 and 5 of the Video for H85. In the video, three fictional countries are introduced, with details of their household incomes. The three countries have obviously different degrees of income inequality.
The Lorenz Curves for the three countries are shown on page 10 of the Video, along with two observations:
One straightforward way to quantify the income concentration is to simply measure the area of the region between the Lorenz Curve \(f(x)\) and the Line of Absolute Equality \(y=x\). In the video, it is pointed out that this region is a simple region, whose top curve is the Line of Absolute Equality and whose bottom curve is the Lorenz Curve: $$top(x)=x \\ bottom(x)=f(x)$$
That is the idea behind the Gini Index, defined as follows:
Definition of the Gini Index of Income Concentration
The Gini Index (GI) for a country is defined to be twice the area of the region bounded by the Lorenz Curve for the country and the Line of Absolute Equality. $$Gini \ Index = GI = 2\cdot \int_0^1 x-f(x)dx$$ Remark: The \(2\) is a scale factor put in so that the Gini Index (GI) will be a number \(0 \leq GI \leq 1\).
Observations:
In general,
You'll work in pairs on a Class Drill about the Gini Index.
A country called Funland has a Lorenz Curve \(f(x)=x^4\). A country called Greatland has a Lorenz Curve \(g(x)=x^5\).
Student #16 Presentation CP3: Show the solution of theClass Drill that the class just worked on. To prepare for this presentation, study
Instructor: Return Exam X3 and discuss common mistakes.
Instructor: Last week, we discussed how to use a definite integral to compute the total change in a quantity in situations where the derivative of the quantity is known. These kinds of problems were called Total Change Problems.
Then, on Monday of this week, we discused how to use a definite integral to compute the area between curves.
And then, on Wednesday of this week, we put those two ideas together, using the area between curves to help illustrate Total Change Problems.
Remember that the topics for those three discussions were all about an important concept in the final month of the course: the equality of three quantities related to area:
Today, and for the rest of the semester, we'll be discussing topics from Section 6.2 of our textbook. That section is about Applications of the Definite Integral in Business and Economics. Today, we will discuss applications of the Area Between Curves to a particular problem in Business, computing what is called the Total Income for a Continuous Income Stream. We will see that this kind of problem is actually just another example of a Total Change Problem.
The expression Continuous Income Stream means that money is flowing into an account with flow rate \(f(t)\) dollars per year. This situation is discussed on pages 4 - 6 of the Notes from the Video for H86. An illustration of money flowing into a bucket (representing the account) is presented there.
A simple question to ask about such a flow is the following:
The answer to the question is that the Total Income is found by integrating the flow rate \(f(t)\).
$$total \ income = TI = \Delta A = A(b) - A(a) = \int_{a}^{b} f(t)dt $$Realize that because the value of the total income (TI) is obtained by integrating the flow rate \(f(t)\), the quantity TI can be visualized as an area between the graph of the flow rate \(f(t)\) and the \(t\) axis. Such an illustration is shown on pages 10 and 16 of the same notes.
You'll work in pairs on a Class Drill about the Total Income from a Continuous Income Stream.
A continuous income stream has flow rate $$f(t) = 2000e^{(0.02t)} \ \text{dollars per year}$$
Student #17 Presentation CP3: Show the solution of the Class Drill that the class just worked on. To prepare for this presentation, study
Instructor: A more complicated situation arises when an income stream is flowing into an account where it will start earning interest upon arrival. This situation is discussed on pages 5 - 8 of the Notes from the Video for H87. An illustration of money flowing into a bucket is again used there. A natural question is
If a continuous income stream flows into an account that earns continuously compounded interest at a rate \(r\), what will be the balance of the account at time \(T\) years? (Note the capital \(T\).) This balance is called the Future Value at time \(T\) years. (abbreviated \(FV\))
The answer to the question is that the Future Value is found by the following integral calculation.
$$future \ value = FV = \int_{0}^{T} f(t)e^{(r(T-t))}dt $$The integral above is rather complicated. For that reason, Barsamian presents the result of the integral in two useful common cases, which are all that is needed for our course.
Particular Result: Future Value of a Continuous Income Stream with Constant Flow If a continuous income stream with flow rate \(f(t)=c\) dollars per year (constant flow) flows into an account that earns continuously compounded interest at rate \(r\), then the balance of the account at time \(T\) years (that is, Future Value (\(FV\)) at time \(T\) years) will be
$$FV=\frac{c\left(e^{(rt)}-1\right)}{r}$$Particular Result: Future Value of a Continuous Income Stream with Exponential Flow If a continuous income stream with flow rate \(f(t)=c \cdot e^{(kt)}\) dollars per year (exponential flow) flows into an account that earns continuously compounded interest at rate \(r\), then the balance of the account at time \(T\) years (that is, Future Value (\(FV\)) at time \(T\) years) will be
$$FV=\frac{c\left(e^{(rt)}-e^{(kt)}\right)}{r-k}$$Instructor: Present this [Example] Future Value of a Continuous Income Stream (For reference, see [Example 2] on page 13 of the Notes from the Video for H87 .) Starting at age \(25\), you deposit \($1000\) a year into an account for retirement. Treat the yearly deposits into the account as a continuous income stream (with constant flow). The money in the account earns \(3\) percent interest, compounded continuously.
Sections, Content, Homework, and Videos:
Students:
Instructor: Review the Grading for the course on the Course Web Page.
Instructor: In this last week of the semester, we'll be continuing to discuss topics from Section 6.2 of our textbook. That section is about Applications of the Definite Integral in Business and Economics. The applications that we will be discussing this week are called Consumers' Surplus, Producers' Surplus, and Equilibrium Price.
Today, we will discuss Consumers' Surplus
Before discussing Consumers' Surplus, however, it is worthwhile to review the Business Terminology of Demand and Price.
Instructor: Review Demand and Price, and discuss why the Demand Price curve is a decreasing curve. (For reference, see pages 2 - 4 of the Notes from the Video for H88)
Instructor: Introduce the Consumers' Surplus (CS) For reference
The Consumers' Surplus, denoted \(CS\), is a quantity that is the total amount that all consumers who are willing to buy the item at the price \(\overline{p}\) will feel like they saved if the selling price is \(\overline{p}\). The Consumers' Surplus (CS) can be visualized as the area between curves on a graph of the Demand Price curve \(D(x)\). Such a visualization is shown on page 10 of the Notes from the Video for H88 .
The value of the Consumers' Surplus (CS) is given by the integral calculation
$$CS=\int_{0}^{\overline{x}}[D(x)-\overline{p} \ ]dx$$In this integral,
Observe that this integral is of the standard form used for computing area between curves. That is,
$$unsigned \ \ area \ = \ USA \ = \int_{a}^{b}top(x) \ - \ bottom(x) \ dx$$Instructor: For the rest of the meeting, you will work on two Class Drills about Consumers' Surplus. Students #15 and #16 will present solutions to the drills after you work on them for awhile..
Suppose that
The goal is to find the value of the Consumers' Surplus (CS) by two methods.
Method 1 (Using Geometry) Do the following:
Method 2 (Using Calculus) Do the following:
Question for the Groups: Do the results obtained by the two methods match?
Student #18 Presentation CP3: Show the solution of Drill Problem #1 that the class just worked on. To prepare for this presentation,
Suppose that
The goal is to illustrate the Consumers' Surplus (CS) using a graph, and then find its value using calculus.
Part 1: Illustrate the Consumers' Surplus Do the following:
Part 2: Find the Value of the Consumers' Surplus Do the following:
Student #19 Presentation CP3: Show the solution of Drill Problem #2 that the class just worked on. To prepare for this presentation,
Instructor: In this last week of the semester, we are discussing topics from Section 6.2 of our textbook. That section is about Applications of the Definite Integral in Business and Economics. The applications that we will are discussing are called Consumers' Surplus, Producers' Surplus, and Equilibrium Price. On Monday, we discussed Consumers' Surplus
Today, we will discuss Producers' Surplus
We start by discussing the Business Terminology of Supply and Price.
Instructor: Discuss Supply and Price, and discuss why the Supply Price curve is an increasing curve. (For reference, see pages 5 - 7 of the Notes from the Video for H89)
Now that we understand the terminology of Supply and Price, we are ready to discuss the Producers' Surplus.
Instructor: Introduce the Producers' Surplus (PS) For reference
The Producers' Surplus, denoted \(PS\), is a quantity that is the total amount that all producers who are willing to supply the item at the price \(\overline{p}\) will feel like they saved if the selling price is \(\overline{p}\). The Producers' Surplus (PS) can be visualized as the area between curves on a graph of the Supply Price curve \(S(x)\). Such a visualization is shown on page 13 of the Notes from the Video for H89 .
The value of the Producers' Surplus (PS) is given by the integral calculation
$$PS=\int_{0}^{\overline{x}}[ \ \overline{p}-S(x)]dx$$In this integral,
Observe that this integral is of the standard form used for computing area between curves. That is,
$$unsigned \ \ area \ = \ USA \ = \int_{a}^{b}top(x) \ - \ bottom(x) \ dx$$Instructor: For the rest of the meeting, you will work on two Class Drills about Producers' Surplus.
Suppose that
The goal is to find the value of the Producers' Surplus (PS) by two methods.
Method 1 (Using Geometry) Do the following:
Method 2 (Using Calculus) Do the following:
Question for the Groups: Do the results obtained by the two methods match?
Student #20 Presentation CP3: Show the solution of Class Drill that the class just worked on. To prepare for this presentation,
Suppose that
The goal is to illustrate the Producers' Surplus (PS) using a graph, and then find its value using calculus.
Part 1: Illustrate the Producers' Surplus Do the following:
Part 2: Find the Value of the Producers' Surplus Do the following:
Instructor: Show the solution of the Class Drill that the class just worked on. (For reference, see [Example 2] on page 17 of the Notes from the Video for H89 .)
Instructor: In this last week of the semester, we are discussing topics from Section 6.2 of our textbook. That section is about Applications of the Definite Integral in Business and Economics. The applications that we will are discussing are called Consumers' Surplus, Producers' Surplus, and Equilibrium Price. On Monday, we discussed Consumers' Surplus; on Wednesday, we discussed Producers' Surplus.
Today, we will discuss Equilibrium Price and Quantity
Instructor: Review the Business Terminology of Price and Demand and Supply.
Instructor: Introduce Equilibrium Price and Quantity (For reference, see pages 8-9 of the Notes from the Video for H90 ). The idea is that in an actual competitive market, the price level for a particular item will be the price at which the quantity that producers are willing to supply equals the quantity that consumers are willing to buy. Since the Demand Price Curve goes down as you move from left to right and the Supply Price Curve goes up, if the two curves cross, they will cross at exactly one point. This point is called the equilibrium price point, and is denoted \( ( \overline{x},\overline{p}) \).
Instructor: For the rest of the meeting, you will work on two Class Drills about Equilibrium Price and Quantity. Students #19 and #20 will present solutions to the drills after you work on them for awhile.
Suppose that
The goal is to find the Equilibrium Price and Quantity, and then find the value of the Consumers' Surplus (CS) and the Producers' Surplus (PS).
Do the following:
Instructor: Show the solution of Class Drill that the class just worked on. (For Reference, see [Example 1] on page 10 of the Notes from the Video for H90.)
Suppose that
The goal is to find the Equilibrium Price and Quantity, and then find the value of the Consumers' Surplus (CS) and the Producers' Surplus (PS).
Do the following:
Instructor: Show the solution of Class Drill that the class just worked on. (For Reference, see [Example 2] on page 16 of the Notes from the Video for H90.)
To the Students: We hope that you have found MATH 1350 to be not just challenging but also rewarding. We wish you success on the Final Exam next week, and in your future time at Ohio University and beyond!
From your Instructor and from Mark Barsamian, the MATH 1350 Coordinator.
Exam X3 lasts the full duration of the Fri Aug 16 class meeting
No Books, no Notes, no Calculators, no Phones, no Smart Watches
The exam material is taken from the material covered in Chapters 5 and 6. See the List of Homework Assignments for links to the corresponding Instructional Videos.
page maintained by Mark Barsamian, last updated May 17, 2024